Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Fuchs, Laszlo
Heinzer, William
and
Olberding, Bruce
2004.
Commutative ideal theory without finiteness conditions: Primal ideals.
Transactions of the American Mathematical Society,
Vol. 357,
Issue. 7,
p.
2771.
Hamilton, Tracy Dawn
2004.
Weak Bourbaki Unmixed Rings: A Step towards Non-Noetherian Cohen-Macaulayness.
Rocky Mountain Journal of Mathematics,
Vol. 34,
Issue. 3,
Heinzer, William
and
Olberding, Bruce
2005.
Unique irredundant intersections of completely irreducible ideals.
Journal of Algebra,
Vol. 287,
Issue. 2,
p.
432.
Fuchs, Laszlo
Heinzer, William
and
Olberding, Bruce
2006.
Commutative ideal theory without finiteness conditions: Completely irreducible ideals.
Transactions of the American Mathematical Society,
Vol. 358,
Issue. 7,
p.
3113.
Olberding, Bruce
2008.
Overrings of two-dimensional Noetherian domains representable by Noetherian spaces of valuation rings.
Journal of Pure and Applied Algebra,
Vol. 212,
Issue. 7,
p.
1797.
RUSH, DAVID E.
2011.
NOETHERIAN SPECTRUM ON RINGS AND MODULES.
Glasgow Mathematical Journal,
Vol. 53,
Issue. 3,
p.
707.
BEHARA, SRINIVAS
and
KUMAR, SHIV DATT
2011.
Group graded associated ideals with flat base change of rings and short exact sequences.
Proceedings - Mathematical Sciences,
Vol. 121,
Issue. 2,
p.
111.
Picavet, Gabriel
2012.
Ascending the divided and going-down properties by absolute flatness.
Arabian Journal of Mathematics,
Vol. 1,
Issue. 1,
p.
113.
Schoutens, Hans
2013.
Dimension and singularity theory for local rings of finite embedding dimension.
Journal of Algebra,
Vol. 386,
Issue. ,
p.
1.
Hummel, Livia
2014.
Commutative Algebra.
p.
195.
Epstein, Neil
and
Shapiro, Jay
2014.
Strong Krull primes and flat modules.
Journal of Pure and Applied Algebra,
Vol. 218,
Issue. 9,
p.
1712.
Quy, Pham Hung
and
Rohrer, Fred
2017.
Injective modules and torsion functors*.
Communications in Algebra,
Vol. 45,
Issue. 1,
p.
285.
Epstein, Neil
and
Shapiro, Jay
2019.
The Ohm–Rush content function II. Noetherian rings, valuation domains, and base change.
Journal of Algebra and Its Applications,
Vol. 18,
Issue. 05,
p.
1950100.
Olberding, Bruce
2021.
Commutative Algebra.
p.
639.
Kourki, Farid
and
Tribak, Rachid
2022.
On seminoetherian rings and modules.
Communications in Algebra,
Vol. 50,
Issue. 12,
p.
5200.
Azarpanah, Fariborz
Ghashghaei, Ebrahim
and
Keshtkar, Zahra
2023.
A closer look at primal and pseudo-irreducible ideals with applications to rings of functions.
Communications in Algebra,
Vol. 51,
Issue. 5,
p.
1907.
Epstein, Neil
2024.
Rings that are Egyptian with respect to a multiplicative set.
Communications in Algebra,
Vol. 52,
Issue. 3,
p.
1277.
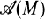 of prime ideals to a module M over a non-Noetherian ring have proven very useful in the past. The most common of these is the set Assf(M) of weak Bourbaki primes of M [2, pp. 289-290].
of prime ideals to a module M over a non-Noetherian ring have proven very useful in the past. The most common of these is the set Assf(M) of weak Bourbaki primes of M [2, pp. 289-290].

