Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-11-20T10:29:52.597Z Has data issue: false hasContentIssue false
  • English
  • Français

Analytic Range Functions of Several Variables

Published online by Cambridge University Press:  20 November 2018

R. Cheng
R. Cheng*
Affiliation:
Department of Mathematics, University of Louisville, Louisville, Kentucky 40292, U.S.A.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let C be a separable Hilbert Space, and let Λ be the halfplane {(m, n) ∈ Ζ2 : m ≥ 1} ∪ {(0, n) ∈ Ζ2 : n ≥ 0} of the integer lattice. Consider the subspace ℳc(Λ) of 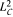on the torus spanned by the C-valued trigonometric functions {Ceims+int : с ∈ C, (m, n) ∈ Λ}. The notion of a Λ-analytic operator on ℳc(Λ) is defined with respect to the family of shift operators {Smn}Λ on ℳC(Λ) given by (Smnƒ)(eis, eit) = eims+intƒ(eis, eit). The corresponding concepts of inner function, outer function and analytic range function are explored. These ideas are applied to the spectral factorization problem in prediction theory.

Keywords

47A6860G25operator valued functioninner functionouter functionanalytic range functionspectral factorization
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 47 , Issue 3 , 01 June 1995 , pp. 462 - 473
Copyright
Copyright © Canadian Mathematical Society 1995

References

1. Cheng, R., Operator valued functions of several variables: Factorization and invariant subspaces, preprint.Google Scholar
2. Cheng, R., Outer factorization of operator valued weight functions on the torus, Studia Math., to appear.Google Scholar
3. Devinatz, D.A., The factorization of operator valued functions, Ann. of Math. (2) 73(1961), 458–495.Google Scholar
4. Helson, H., Lectures on Invariant Subspaces, Academic Press, New York, 1964.Google Scholar
5. Helson, H. and Lowdenslager, D., Prediction theory and Fourier Series in several variables I, II, Acta Math. 99(1958), 165–202. ibid. 106(1961), 175–213.Google Scholar
6. Korezlioglu, H. and Ph. Loubaton, Spectral factorization of wide sense stationary processes on p, J. Multivariate Anal. 19(1986), 24–47.Google Scholar
7. Loubaton, Ph., A regularity criterion for lexicographical prediction of multivariate wide-sense stationary processes on Ζ2 with non-full-rank spectral densities, J. Funct. Anal. 104(1992), 198–228.Google Scholar
8. Lowdenslager, D., On factoring matrix valued functions, Ann. of Math. (2) 78(1963), 450–454.Google Scholar
9. Rosenblum, M., Vectorial Toeplitz operators and the Féjér-Riesz theorem, J. Math. Anal. Appl. 23(1968), 139–147.Google Scholar
10. Rosenblum, M. and Rovnyak, J., Hardy Classes and Operator Theory, Oxford University Press, New York, 1985.Google Scholar