Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-11-27T21:47:51.507Z Has data issue: false hasContentIssue false
  • English
  • Français

Analytic Properties of Power Product Expansions

Published online by Cambridge University Press:  20 November 2018

H. Gingold  and
A. Knopfmacher
H. Gingold
Affiliation:
Department of Mathematics West Virginia University Morgantown, West Virginia 26506 U.S.A.
A. Knopfmacher
Affiliation:
Department of Computational and Applied Mathematics University of the Witwatersrand Johannesburg, P.O. Wits 2050 South Africa e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let ƒ(z) be a complex function analytic in some neighbourhood of the origin with ƒ(0) = 1. It is known that ƒ(z) admits a unique "power product" expansion of the form 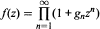convergent near zero. We derive a simple direct bound for the radius of convergence of this product expansion in terms of the coefficients of ƒ(z). In addition we show that the same bound holds in the case of "inverse power product" expansions 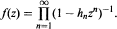Examples are given for which these bounds are sharp. We show also that products with nonnegative coefficients have the same radius of convergence as their corresponding series.

Keywords

41A1030E10
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 47 , Issue 6 , 01 December 1995 , pp. 1219 - 1239
Copyright
Copyright © Canadian Mathematical Society 1995

References

[BL] Borwein, J. and Lou, S., Asymptotics of a Sequence of Witt Vectors, J. Approx. Theory 69(1992), 326–337.Google Scholar
[DS] Dress, A.W.M. and Siebeneicher, C., The Burnside Ring of the Infinite Cyclic Group and its Relations to the Necklace Algebra, ƛ-Rings and the Universal Ring of Witt Vectors, Adv. in Math. 78(1989), 1–1.Google Scholar
[F] Feld, J.M., The Expansion of Analytic Functions in Generalised Lambert Series, Ann. of Math. 33(1932), 139–142.Google Scholar
[G] Grosswald, E., Topics from the Theory of Numbers, 2nd Edition, Birkhäuser, 1984.Google Scholar
[GGM] Gingold, H., Gould, H.W. and Mays, M.E., Power Product Expansions, Utilitas Math. 34(1988), 143–167.Google Scholar
[GKL] Gingold, H., Knopfmacher, A. and Lubinsky, D.S., The Zero Distribution of the Partial Products of Power Product Expansions, Analysis 13(1993), 133–157.Google Scholar
[GK] Greene, D.H. and Knuth, D.E., Mathematics for the Analysis of Algorithms, Third Edition, Birkhauser, 1990.Google Scholar
[IW] Indlekofer, H. and Warlimont, R., Remarks on the Infinite Product Representations of Holomorphic Function, Publ. Math. Debrecen 41(1992), 263–276.Google Scholar
[K] Knopfmacher, A., Infinite Product Factorizations of Analytic Functions, J. Math. Anal. Appl. 162(1991), 526–536.Google Scholar
[KKR] Knopfmacher, A., Knopfmacher, J. and Ridley, J.N., Unique Factorizations of Formal Power Series,, J. Math. Anal. Appl. 149(1990), 402–411.Google Scholar
[KL] Knopfmacher, A. and Lucht, L., The Radius of Convergence of Power Product Expansions, Analysis 11(1991), 91–99.Google Scholar
[KORSW] Knopfmacher, A., Odlyzko, A.M., Richmond, B., Szekeres, G. and Wormald, N., On Set Partitions with Unequal Block Sizes, preprint.Google Scholar
[KR] Knopfmacher, A. and Ridley, J.N., Reciprocal Sums Over Partitions and Compositions, SIAMJ. Discrete Math. 6(1993), 388–399.Google Scholar
[Kn] Knopp, K., Theory and Application of Infinite Series, 2nd English Edition, Blackie, Glasgow, London, 1951.Google Scholar
[R] Ritt, J.F., Representation of Analytic Functions in Infinite Product Expansions, Math. Z. 32(1930), 1–3.Google Scholar