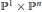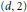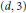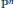Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Abo, Hirotachi
2010.
On non-defectivity of certain Segre–Veronese varieties.
Journal of Symbolic Computation,
Vol. 45,
Issue. 12,
p.
1254.
Bernardi, Alessandra
Carlini, Enrico
and
Catalisano, Maria Virginia
2011.
Higher secant varieties of Pn×Pm embedded in bi-degree (1,d).
Journal of Pure and Applied Algebra,
Vol. 215,
Issue. 12,
p.
2853.
Ballico, Edoardo
Bernardi, Alessandra
and
Catalisano, Maria Virginia
2012.
Higher Secant Varieties of ℙn × ℙ1Embedded in Bi-Degree (a,b).
Communications in Algebra,
Vol. 40,
Issue. 10,
p.
3822.
Laface, Antonio
and
Postinghel, Elisa
2013.
Secant varieties of Segre-Veronese embeddings of $$(\mathbb{P }^1)^r$$.
Mathematische Annalen,
Vol. 356,
Issue. 4,
p.
1455.
Abo, Hirotachi
and
Wan, Jia
2013.
On Waringʼs problem for systems of skew-symmetric forms.
Linear Algebra and its Applications,
Vol. 439,
Issue. 8,
p.
2330.
Abo, Hirotachi
and
Brambilla, Maria Chiara
2013.
On the dimensions of secant varieties of Segre-Veronese varieties.
Annali di Matematica Pura ed Applicata,
Vol. 192,
Issue. 1,
p.
61.
Carlini, Enrico
Grieve, Nathan
and
Oeding, Luke
2014.
Connections Between Algebra, Combinatorics, and Geometry.
Vol. 76,
Issue. ,
p.
101.
Bernardi, Alessandra
Carlini, Enrico
Catalisano, Maria Virginia
Gimigliano, Alessandro
and
Oneto, Alessandro
2018.
The Hitchhiker Guide to: Secant Varieties and Tensor Decomposition.
Mathematics,
Vol. 6,
Issue. 12,
p.
314.
Ventura, Emanuele
2019.
Real rank boundaries and loci of forms.
Linear and Multilinear Algebra,
Vol. 67,
Issue. 7,
p.
1404.
Catalisano, Maria Virginia
and
Oneto, Alessandro
2020.
Tangential varieties of Segre–Veronese surfaces are never defective.
Revista Matemática Complutense,
Vol. 33,
Issue. 1,
p.
295.
Ballico, Edoardo
2022.
On the secant varieties of tangential varieties.
Journal of Pure and Applied Algebra,
Vol. 226,
Issue. 12,
p.
107132.
Galuppi, Francesco
and
Oneto, Alessandro
2022.
Secant non-defectivity via collisions of fat points.
Advances in Mathematics,
Vol. 409,
Issue. ,
p.
108657.