Research Article
A Class of functional equations which have entire solutions
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 351-356
-
- Article
-
- You have access
- Export citation
A diophantine inequality with prime variables
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 57-66
-
- Article
-
- You have access
- Export citation
Fractional integration and the hyperbolic derivative
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 357-364
-
- Article
-
- You have access
- Export citation
Fubini's theorem for Radon polymeasures
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 221-229
-
- Article
-
- You have access
- Export citation
A Discrete calculus of variations algorithm
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 365-371
-
- Article
-
- You have access
- Export citation
The limiting behaviour of certain sequences of continued fractions
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 67-76
-
- Article
-
- You have access
- Export citation
Almost periodic solutions of nonlinear parabolic equations
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 231-238
-
- Article
-
- You have access
- Export citation
Contracted primes of the complete ring of quotients
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 373-375
-
- Article
-
- You have access
- Export citation
On Mosco convergence of convex sets
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 239-253
-
- Article
-
- You have access
- Export citation
A note on annihilator Banach algebras
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 77-81
-
- Article
-
- You have access
- Export citation
A convergence property of Dubins' representation of distributions
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 83-85
-
- Article
-
- You have access
- Export citation
Reflections and symmetries in compact symmetric spaces
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 377-386
-
- Article
-
- You have access
- Export citation
Oscillatory properties of the solutions of linear equations of neutral type
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 255-261
-
- Article
-
- You have access
- Export citation
A topological zero-one law for open continuous maps
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 263-266
-
- Article
-
- You have access
- Export citation
Approximation by fourier stieltjes series
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 87-92
-
- Article
-
- You have access
- Export citation
Characterisation of a multivariate stochastic ordering
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 387-392
-
- Article
-
- You have access
- Export citation
On commutativity of associative rings
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 267-271
-
- Article
-
- You have access
- Export citation
A note on compact sets in spaces of subsets
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 393-395
-
- Article
-
- You have access
- Export citation
Rings isomorphic to their unbounded left ideals
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 93-94
-
- Article
-
- You have access
- Export citation
On the lattice of right ideals of the endomorphism ring of an abelian group
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 273-291
-
- Article
-
- You have access
- Export citation

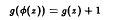
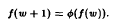
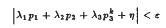
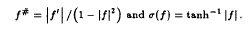
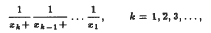

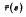 are non- decreasing and
are non- decreasing and  .
.