Research Article
On tidy subgroups of locally compact totally disconnected groups
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 485-490
-
- Article
-
- You have access
- Export citation
Vanishing of the integral of the Hurwitz zeta Function
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 121-127
-
- Article
-
- You have access
- Export citation
Some weighted estimates for imaginary powers of Laplace operators
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 129-135
-
- Article
-
- You have access
- Export citation
Hausdorff dimension of random fractals with overlaps
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 315-328
-
- Article
-
- You have access
- Export citation
Nondualisable semigroups
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 491-502
-
- Article
-
- You have access
- Export citation
Free surface waves over a depression
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 329-335
-
- Article
-
- You have access
- Export citation
Formulae associated with 5, 7, 9 and 11 squares
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 503-510
-
- Article
-
- You have access
- Export citation
Maximal (k, l)-free sets in ℤ/pℤ are arithmetic progressions
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 137-144
-
- Article
-
- You have access
- Export citation
Multipliers on weighted function spaces over locally compact vilenkin groups
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 337-351
-
- Article
-
- You have access
- Export citation
Gröbner bases and products of coefficient rings
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 145-152
-
- Article
-
- You have access
- Export citation
The average distance property of classical Banach spaces II
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 511-520
-
- Article
-
- You have access
- Export citation
The Kunze–Stein phenomenon on the isometry group of a tree
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 153-174
-
- Article
-
- You have access
- Export citation
Front matter
BAZ volume 65 issue 2 Cover and Front matter
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Research Article
The compositional inverse of a class of permutation polynomials over a finite field
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 521-526
-
- Article
-
- You have access
- Export citation
Abstracts of Australasian Ph.D. Theses
Summary fucntions in the analysis of spatial point patterns
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 527-528
-
- Article
-
- You have access
- Export citation
Back matter
BAZ volume 65 issue 2 Cover and Back matter
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation
Abstracts of Australasian Ph.D. Theses
Cuspidal modules of finite general linear group
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 175-176
-
- Article
-
- You have access
- Export citation
Front matter
BAZ volume 65 issue 3 Cover and Front matter
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. f1-f6
-
- Article
-
- You have access
- Export citation
BAZ volume 65 issue 1 Cover and Front matter
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back matter
BAZ volume 65 issue 3 Cover and Back matter
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation

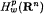 to weighted Lebesgue spaces
to weighted Lebesgue spaces 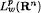 where 0 <
where 0 < 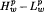 estimates for these operators when 0 <
estimates for these operators when 0 < 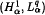 multiplier result. Then we give an
multiplier result. Then we give an 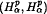 multiplier result under a similar condition of Lu-Yang type. In Section 3, we obtain a result about the boundedness of multipliers on weighted Besov spaces.
multiplier result under a similar condition of Lu-Yang type. In Section 3, we obtain a result about the boundedness of multipliers on weighted Besov spaces.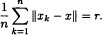
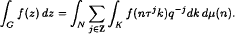
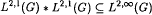 and that a related maximal operator on is bounded from
and that a related maximal operator on is bounded from