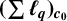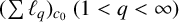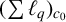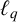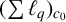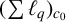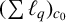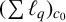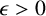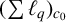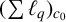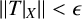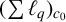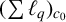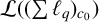Research Article
A NEW NONLOCAL NONLINEAR DIFFUSION EQUATION: THE ONE-DIMENSIONAL CASE
- Part of:
-
- Published online by Cambridge University Press:
- 05 May 2022, pp. 333-339
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THE MAXIMAL IDEAL IN THE SPACE OF OPERATORS ON
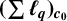 $\boldsymbol {(\sum {\ell }_{q})_{c_{0}}}$
$\boldsymbol {(\sum {\ell }_{q})_{c_{0}}}$
- Part of:
-
- Published online by Cambridge University Press:
- 21 February 2022, pp. 340-348
-
- Article
- Export citation
Abstracts of Australasian PhD Theses
MULTIPLE IMPUTATION FOR CATEGORICAL VARIABLES IN MULTILEVEL DATA
- Part of:
-
- Published online by Cambridge University Press:
- 04 August 2022, pp. 349-350
-
- Article
-
- You have access
- HTML
- Export citation
SOME CONTRIBUTIONS TO MEASURING AND UNDERSTANDING HETEROGENEITY IN META-ANALYSIS
- Part of:
-
- Published online by Cambridge University Press:
- 15 June 2022, pp. 351-352
-
- Article
-
- You have access
- HTML
- Export citation
Front Cover (OFC, IFC) and matter
BAZ volume 106 issue 2 Cover and Front matter
-
- Published online by Cambridge University Press:
- 05 September 2022, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back Cover (OBC, IBC) and matter
BAZ volume 106 issue 2 Cover and Back matter
-
- Published online by Cambridge University Press:
- 05 September 2022, pp. b1-b2
-
- Article
-
- You have access
- Export citation