It is shown that if a retarded delay differential equation has a global attractor 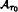 in the space C ([—τ0, ], ℝd) for a given nonzero constant delay τ0, then the equation has an attractor Aτ in the space C ([—τ, 0], ℝd) for nearby constant delays τ. Moreover the attractors Aτ converge upper semi continuously to
in the space C ([—τ0, ], ℝd) for a given nonzero constant delay τ0, then the equation has an attractor Aτ in the space C ([—τ, 0], ℝd) for nearby constant delays τ. Moreover the attractors Aτ converge upper semi continuously to 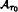 in C ([—τ0, 0], ℝd) in the sense that they are identified through corresponding segments of entire trajectories in ℝd with nonempty compact subsets
in C ([—τ0, 0], ℝd) in the sense that they are identified through corresponding segments of entire trajectories in ℝd with nonempty compact subsets 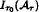 of C ([—τ0, 0], ℝd) which converge upper semi continuously to
of C ([—τ0, 0], ℝd) which converge upper semi continuously to 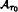 in C ([—τ0, 0], ℝd).
in C ([—τ0, 0], ℝd).