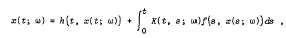Research Article
Isomorphisms of some convolution algebras and their multiplier algebras
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 321-335
-
- Article
-
- You have access
- Export citation
Mean-square stability of a class of stochastic integral equations
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 337-352
-
- Article
-
- You have access
- Export citation
Transversals of squares
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 353-358
-
- Article
-
- You have access
- Export citation
Epireflection operators vs perfect morphisms and closed classes of epimorphisms
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 359-366
-
- Article
-
- You have access
- Export citation
Remainders of metric completions
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 367-376
-
- Article
-
- You have access
- Export citation
On the relation of a distributive lattice to its lattice of ideals
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 377-385
-
- Article
-
- You have access
- Export citation
A note on flabby sheaves
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 387-389
-
- Article
-
- You have access
- Export citation
On three-Engel groups
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 391-405
-
- Article
-
- You have access
- Export citation
Free generators in free inverse semigroups
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 407-424
-
- Article
-
- You have access
- Export citation
Representation of a function in terms of its mean boundary values
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 425-427
-
- Article
-
- You have access
- Export citation
Maximal perfect spaces
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 429-436
-
- Article
-
- You have access
- Export citation
On varieties of soluble groups II
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 437-441
-
- Article
-
- You have access
- Export citation
Bounded approximate identities and tensor products
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 443-445
-
- Article
-
- You have access
- Export citation
Abstracts of Australasian Ph.D. theses
The effect of beam seas on a stationary ship in shallow water
-
- Published online by Cambridge University Press:
- 17 April 2009, p. 447
-
- Article
-
- You have access
- Export citation
Bases of projections in Banach spaces with an appendix on non-standard analysis
-
- Published online by Cambridge University Press:
- 17 April 2009, p. 448
-
- Article
-
- You have access
- Export citation
Phase measurements and narrow spectral band inference
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 449-450
-
- Article
-
- You have access
- Export citation
Inference problems for vector linear time series models
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 451-452
-
- Article
-
- You have access
- Export citation
Almost periodic and quasi-periodic solutions of differential equations
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 453-454
-
- Article
-
- You have access
- Export citation
The analytic properties of the triangle and box diagram amplitudes
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 455-456
-
- Article
-
- You have access
- Export citation
Subnormal structure in infinite soluble groups
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 457-458
-
- Article
-
- You have access
- Export citation