Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-26T05:45:07.775Z Has data issue: false hasContentIssue false
  • English
  • Français

Transversals of squares

Published online by Cambridge University Press:  17 April 2009

N.H. Williams
N.H. Williams
Affiliation:
Department of Mathematics, Monash University, Clayton, Victoria.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let κ and λ be cardinal numbers. Take any family A = {Aν; ν ∈ N} where each Aν is a product Aν = Bν x Cν with |Bν = |Cν| = Nα, such that if B x C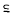Aμ x Aν (for μ ≠ ν) then |B|, |c| < λ. We investigate under what conditions on α, κ, λ and |N| there will be a set T with 1 ≤ |T∩Aν| < κ for each ν.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 7 , Issue 3 , December 1972 , pp. 353 - 358
Copyright
Copyright © Australian Mathematical Society 1972

References

[1]Endös, P. and Hajnal, A., “On a property of families of sets”, Acta Math. Acad. Sci. Hungar. 12 (1961), 87–123.Google Scholar
[2]Tarski, Alfred, “Sur la décomposition des ensembles en sous-ensembles presque disjoints”, Fund. Math. 14 (1929), 205–215.Google Scholar