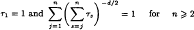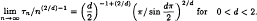Research Article
Inverse shadowing of circle maps
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 353-359
-
- Article
-
- You have access
- Export citation
A note on Cohn's universal localisation at a semiprime ideal
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 361-367
-
- Article
-
- You have access
- Export citation
A noncommutative half-angle formula
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 369-382
-
- Article
-
- You have access
- Export citation
On the n-parameter abstract Cauchy problem
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 383-394
-
- Article
-
- You have access
- Export citation
Inverse semigroups all of whose proper homomorphic images are groups
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 395-401
-
- Article
-
- You have access
- Export citation
A fast algorithm for curve singularities
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 403-414
-
- Article
-
- You have access
- Export citation
On the existence of premixed laminar flames
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 415-427
-
- Article
-
- You have access
- Export citation
A note on the roots of trinomials over a finite field
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 429-432
-
- Article
-
- You have access
- Export citation
Witt kernels of bi-quadratic extensions in characteristic 2
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 433-440
-
- Article
-
- You have access
- Export citation
Groups in which every subgroup is modular-by-finite
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 441-450
-
- Article
-
- You have access
- Export citation
The day norm and Gruenhage compacta
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 451-456
-
- Article
-
- You have access
- Export citation
Centre and norm
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 457-464
-
- Article
-
- You have access
- Export citation
Reverses of the Cauchy–Bunyakovsky–Schwarz inequality for n-tuples of complex numbers
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 465-480
-
- Article
-
- You have access
- Export citation
The asymptotic growth of integer solutions to the Rosenberger equations
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 481-497
-
- Article
-
- You have access
- Export citation
Operator ideals and tensor norms defined by a sequence space
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 499-517
-
- Article
-
- You have access
- Export citation
An inequality with application to a difference equation
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 519-528
-
- Article
-
- You have access
- Export citation
Front matter
BAZ volume 69 issue 3 Cover and Front matter
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. f1-f6
-
- Article
-
- You have access
- Export citation
Back matter
BAZ volume 69 issue 3 Cover and Back matter
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation

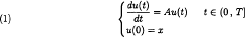
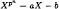 , with
, with 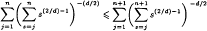 holds for
holds for