Research Article
Some bounds for the degree of commutativity of a p-group of maximal class
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 353-367
-
- Article
-
- You have access
- Export citation
Extension of Hölder's inequality (I)
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 369-375
-
- Article
-
- You have access
- Export citation
On additive maps of prime rings
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 377-381
-
- Article
-
- You have access
- Export citation
Some series involving the zeta function
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 383-393
-
- Article
-
- You have access
- Export citation
Strange triangular maps of the square
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 395-415
-
- Article
-
- You have access
- Export citation
A simple proof of the Beckenbach-Lorentz inequality
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 417-420
-
- Article
-
- You have access
- Export citation
The cohomology rings of finite groups with semi-dihedral Sylow 2-subgroups
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 421-432
-
- Article
-
- You have access
- Export citation
On strongly pi-regular rings of stable range one
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 433-437
-
- Article
-
- You have access
- Export citation
Chaos in sociobiology
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 439-451
-
- Article
-
- You have access
- Export citation
On an extension of Hölder's inequality
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 453-458
-
- Article
-
- You have access
- Export citation
A note on periodic points and recurrent points of maps of dendrites
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 459-461
-
- Article
-
- You have access
- Export citation
An imbedding theorem for anisotropic Orlicz-Sobolev spaces
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 463-467
-
- Article
-
- You have access
- Export citation
Natural duality via a finite set of relations
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 469-478
-
- Article
-
- You have access
- Export citation
A right continuous right weakly si-ring is semisimple
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 479-488
-
- Article
-
- You have access
- Export citation
Totally disconnected groups and proofs of conjectures of Hofmann and Mukherjea
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 489-494
-
- Article
-
- You have access
- Export citation
A note on growth sequences of finite simple groups
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 495-499
-
- Article
-
- You have access
- Export citation
Implicit parabolic differential equations
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 501-509
-
- Article
-
- You have access
- Export citation
A link between two characterisations of complete matrix rings
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 511-516
-
- Article
-
- You have access
- Export citation
A generalisation of Ahlfors-Schwarz lemma to Riemannian geometry
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 517-520
-
- Article
-
- You have access
- Export citation
The fit and flat components of barrelled spaces
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 521-528
-
- Article
-
- You have access
- Export citation

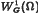 of weakly differentiable functions
of weakly differentiable functions 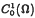 in the norm ∥
in the norm ∥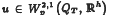 (
(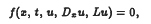
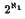 in
in