Hostname: page-component-745bb68f8f-mzp66 Total loading time: 0 Render date: 2025-02-10T15:42:51.806Z Has data issue: false hasContentIssue false
  • English
  • Français

The fit and flat components of barrelled spaces

Published online by Cambridge University Press:  17 April 2009

Stephen A. Saxon  and
Ian Tweddle
Stephen A. Saxon
Affiliation:
Department of Mathematics, University of Florida, PO Box 118000, Gainesville FL 32611–8000, United States of America
Ian Tweddle
Affiliation:
Department of Mathematics, University of Strathclyde, Glasgow G1 1XH, Scotland, United Kingdom
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The Splitting Theorem says that any given Hamel basis for a (Hausdorff) barrelled space E determines topologically complementary subspaces Ec and ED, and that Ec is flat, that is, contains no proper dense subspace. By use of this device it was shown that if E is non-flat it must contain a dense subspace of codimension at least ℵ0; here we maximally increase the estimate to ℵ1 under the assumption that the dominating cardinal ∂ equals ℵ1 [strictly weaker than the Continuum Hypothesis (CH)]. A related assumption strictly weaker than the Generalised CH allows us to prove that ED is fit, that is, contains a dense subspace whose codimension in ED is dim (ED), the largest imaginable. Thus the two components are extreme opposites, and E itself is fit if and only if dim (ED) ≥ dim (Ec), in which case there is a choice of basis for which ED = E. 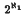Morover, E is non-flat (if and) only if the codimension of E′ is at least in E*. These results ensure latitude in the search for certain subspaces of E* transverse to E′, as in the barrelled countable enlargement (BCE) problem, and show that every non-flat GM-space has a BCE.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 51 , Issue 3 , June 1995 , pp. 521 - 528
Copyright
Copyright © Australian Mathematical Society 1995

References

[1]van Douwen, E.K, ‘The integers and topology’, in Handbook of Set-theoretic Topology, (Kunen, K. and Vaughan, J.E., Editors) (North-Holland, 1984), pp. 111–168.CrossRefGoogle Scholar
[2]Eberhardt, V. and Roelcke, W., ‘Über einen Graphensatz für lineare Abbildungen mit metrisierbarem Zielraum’, Manuscripta Math. 13 (1974), 53–68.CrossRefGoogle Scholar
[3]Robertson, W.J., Saxon, S.A. and Robertson, A.P., ‘Barrelled spaces and dense vector subspaces’, Bull. Austral. Math. Soc. 37 (1988), 383–388.CrossRefGoogle Scholar
[4]Robertson, W.J., Tweddle, I. and Yeomans, F.E., ‘On the stability of barrelled topologies III’, Bull. Austral. Math. Soc. 22 (1980), 99–112.CrossRefGoogle Scholar
[5]Saxon, S.A., ‘The codensity character of topological vector spaces’, in Topological vector spaces, algebras and related areas, (Lau, A. and Tweddle, I., Editors) (Longman, 1994), pp. 24–36.Google Scholar
[6]Saxon, S.A. and Robertson, W.J., ‘Dense barrelled subspaces of uncountable codimension’, Proc. Amer. Math. Soc. 107 (1989), 1021–1029.CrossRefGoogle Scholar
[7]Saxon, S.A. and Ruiz, L.M. Sánchez, ‘Optimal cardinals for metrizable barrelled spaces’, J. London Math. Soc. (to appear).Google Scholar
[8]Saxon, S.A. and Ruiz, L.M. Sánchez, ‘Barrelled countable enlargements and the bounding cardinal’, J. London Math Soc. (to appear).Google Scholar
[9]Saxon, S.A. and Ruiz, L.M. Sánchez, ‘Barrelled countable enlargements and the dominating cardinal’, (preprint).Google Scholar
[10]Tweddle, I., Saxon, S.A. and Ruiz, L.M. Sánchez, ‘Barrelled countable enlargements’, in Topological vector spaces, algebras and related areas, (Lau, A. and Tweddle, I., Editors) (Longman, 1994), pp. 3–15.Google Scholar