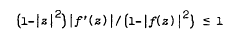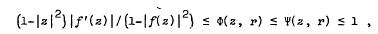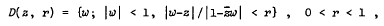Research Article
On second derivative estimates for equations of Monge-Ampère type
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 321-334
-
- Article
-
- You have access
- Export citation
Does the Frobenius endomorphism always generate a direct summand in the endomorphism monoids of fields of prime characteristic?
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 335-356
-
- Article
-
- You have access
- Export citation
On orthogonally decomposable ordered Banach spaces
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 357-380
-
- Article
-
- You have access
- Export citation
An effective seven cube theorem
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 381-385
-
- Article
-
- You have access
- Export citation
An oscillation theorem for sublinear elliptic differential inequalities
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 387-394
-
- Article
-
- You have access
- Export citation
Meromorphic starlike univalent functions
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 395-410
-
- Article
-
- You have access
- Export citation
Elementary properties of vector space graphs
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 411-420
-
- Article
-
- You have access
- Export citation
Conditional expectation for operator-valued measures and functions
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 421-429
-
- Article
-
- You have access
- Export citation
On the codimension of a minimal immersion
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 431-433
-
- Article
-
- You have access
- Export citation
Exponential dichotomy of strongly discontinuous semigroups
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 435-448
-
- Article
-
- You have access
- Export citation
An existence theorem for ordinary differential equations in Banach spaces
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 449-456
-
- Article
-
- You have access
- Export citation
Length and area inequalities for the derivative of a bounded and holomorphic function
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 457-462
-
- Article
-
- You have access
- Export citation
A general denseness result for relaxed control theory
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 463-475
-
- Article
-
- You have access
- Export citation
Abstract of Australasian PhD Thesis
Solutions of field equations in general relativity with spinor connection
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 477-479
-
- Article
-
- You have access
- Export citation
Author Index
Author Index Volumes 21 (1980) To 30 (1984)
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 481-510
-
- Article
-
- You have access
- Export citation
Front matter
BAZ volume 30 issue 3 Cover and Front matter
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. f1-f4
-
- Article
-
- You have access
- Export citation
Back matter
BAZ volume 30 issue 3 Cover and Back matter
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. b1-b3
-
- Article
-
- You have access
- Export citation

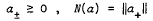 and
and 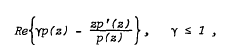
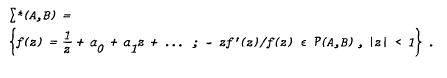
 of S
of S