Hostname: page-component-78c5997874-s2hrs Total loading time: 0 Render date: 2024-11-10T03:11:03.617Z Has data issue: false hasContentIssue false
  • English
  • Français

Elementary properties of vector space graphs

Published online by Cambridge University Press:  17 April 2009

Grace Orzech
Grace Orzech
Affiliation:
Department of Mathematics and Statistics, Queen's University, Kingston, Ontario, Canada K7L 3N6.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let SΓ be a vector space graph. A graphic subspace 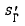of SΓ need not be a direct summand with a graphic complement. A necessary and sufficient condition for the existence of a graphic complement is given. Also, it is shown that every graphic subspace 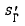possesses an o-special basis which extends to an o-special basis of SΓ.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 30 , Issue 3 , December 1984 , pp. 411 - 420
Copyright
Copyright © Australian Mathematical Society 1984

References

[1]Curtis, C.W. and Reiner, I., Representation theory of finite groups and associative algebras (Interscience, New York, 1962).Google Scholar
[2]Ribenboim, P., “Vector space graphs”, Nanta Math. 12 (1979), 125–132.Google Scholar