Research Article
Nilpotency and related properties of group extensions
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 145-154
-
- Article
-
- You have access
- Export citation
A homomorphism theorem for projective planes
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 155-158
-
- Article
-
- You have access
- Export citation
A universal semigroup
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 159-161
-
- Article
-
- You have access
- Export citation
Rings with orthogonality relations
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 163-178
-
- Article
-
- You have access
- Export citation
The weak density of the non-invertible elements of a commutative Banach algebra
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 179-182
-
- Article
-
- You have access
- Export citation
On properties of countable character
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 183-192
-
- Article
-
- You have access
- Export citation
A characterization of Banach-star-algebras by numerical range
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 193-200
-
- Article
-
- You have access
- Export citation
On the semigroup of all continuous linear mappings on a Banach space
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 201-203
-
- Article
-
- You have access
- Export citation
Generalization of Hall planes of odd order
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 205-209
-
- Article
-
- You have access
- Export citation
Locally finite varieties of groups arising from Cross varieties
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 211-215
-
- Article
-
- You have access
- Export citation
Maximal sum-free sets in finite abelian groups
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 217-223
-
- Article
-
- You have access
- Export citation
Geodesies of an affine connection and electromagnetism with radiation reaction
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 225-240
-
- Article
-
- You have access
- Export citation
A dimension formula relating to algebraic groups
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 241-245
-
- Article
-
- You have access
- Export citation
Certain non-algebras in harmonic analysis
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 247-254
-
- Article
-
- You have access
- Export citation
Functions of asymptotic expansions
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 255-258
-
- Article
-
- You have access
- Export citation
Convergence criteria for Fourier series
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 259-262
-
- Article
-
- You have access
- Export citation
The interrelations among various spaces of distributions
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 263-271
-
- Article
-
- You have access
- Export citation
A note on order paracompactness
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 273-279
-
- Article
-
- You have access
- Export citation
Abstracts of Australasian Ph.D. theses
(Lp, Lq)-multiplier problems
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 281-282
-
- Article
-
- You have access
- Export citation
Wild knots and arcs in 3-space
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 283-284
-
- Article
-
- You have access
- Export citation

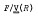 the answer is “yes” for the stronger properties considered, but for the weaker ones the question remains open.
the answer is “yes” for the stronger properties considered, but for the weaker ones the question remains open.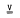 be a Cross variety and let
be a Cross variety and let 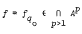 and
and 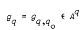 are constructed such that
are constructed such that 
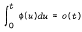 ,
,