Research Article
On finite G-locally primitive graphs and the Weiss conjecture
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 353-356
-
- Article
-
- You have access
- Export citation
Maximal averages along curves over the p-adic numbers
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 357-375
-
- Article
-
- You have access
- Export citation
Pointed Blaschke manifolds and geodesic normal sections
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 377-383
-
- Article
-
- You have access
- Export citation
The similarity problem for tensor products of certain C*-algebras
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 385-389
-
- Article
-
- You have access
- Export citation
On the orders of generators of capable p-groups
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 391-395
-
- Article
-
- You have access
- Export citation
A remark on preinvex functions
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 397-400
-
- Article
-
- You have access
- Export citation
On the injectivity of the Vassiliev homomorphism of singular Artin monoids
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 401-422
-
- Article
-
- You have access
- Export citation
Two necessary and sufficient conditions for Möbius subgroups to be g-discontinuous
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 423-427
-
- Article
-
- You have access
- Export citation
Existence and L∞ estimates for a class of singular ordinary differential equations
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 429-440
-
- Article
-
- You have access
- Export citation
Polynomial near-rings in k indeterminates
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 441-449
-
- Article
-
- You have access
- Export citation
Quadratic reverses of the triangle inequality for Bochner integral in Hilbert spaces
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 451-462
-
- Article
-
- You have access
- Export citation
Diametrically contractive mappings
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 463-468
-
- Article
-
- You have access
- Export citation
A counterexample using 4-linear forms
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 469-473
-
- Article
-
- You have access
- Export citation
A note on Lagrange interpolation for |x|λ at equidistant nodes
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 475-480
-
- Article
-
- You have access
- Export citation
Abelian groups as inner mapping groups of loops
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 481-488
-
- Article
-
- You have access
- Export citation
A note on a continued fraction of Ramanujan
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 489-497
-
- Article
-
- You have access
- Export citation
Stability of Dhombres' equation
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 499-505
-
- Article
-
- You have access
- Export citation
Properly embedded and immersed minimal surfaces in the Heisenberg group
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 507-520
-
- Article
-
- You have access
- Export citation
Hardy-type inequalities for means
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 521-528
-
- Article
-
- You have access
- Export citation
Index
Bulletin of the Australian Mathematical Society Author Index, Volume 61 (2000) – 70 (2004)
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 529-561
-
- Article
-
- You have access
- Export citation

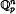 defined by
defined by 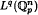 bounded, where 1 <
bounded, where 1 < 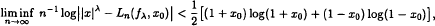 where λ > 0, λ ≠ 2, 4, … and
where λ > 0, λ ≠ 2, 4, … and 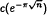 for various positive integers
for various positive integers 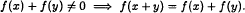 This paper is devoted to the stability of the above equation.
This paper is devoted to the stability of the above equation.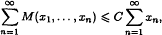 ,
Where
,
Where