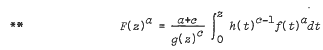Research Article
What is the theory of shape?
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 161-198
-
- Article
-
- You have access
- Export citation
Murskii's algebra does not satisfy min
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 199-203
-
- Article
-
- You have access
- Export citation
A new definition of variational derivative
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 205-210
-
- Article
-
- You have access
- Export citation
A note on the concept of multiset
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 211-217
-
- Article
-
- You have access
- Export citation
On solutions of parabolic equations in regions with edges
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 219-230
-
- Article
-
- You have access
- Export citation
On generalized Nörlund methods of summability II
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 231-239
-
- Article
-
- You have access
- Export citation
On starlike functions
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 241-247
-
- Article
-
- You have access
- Export citation
The relative Schoenflies theorem
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 249-251
-
- Article
-
- You have access
- Export citation
Generalized absolute continuity of a function of Wiener's class
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 253-258
-
- Article
-
- You have access
- Export citation
Minimal requirements for Minkowski's theorem in the plane I
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 259-274
-
- Article
-
- You have access
- Export citation
Minimal requirements for Minkowski's theorem in the plane II
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 275-283
-
- Article
-
- You have access
- Export citation
Some commutativity results for rings
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 285-289
-
- Article
-
- You have access
- Export citation
Metric projections and the differentiability of distance functions
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 291-312
-
- Article
-
- You have access
- Export citation
Abstracts of Australasian PhD Theses
On regular semigroups, semirings and rings
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 313-314
-
- Article
-
- You have access
- Export citation
Primitive permutation groups containing a cycle of prime-power length
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 315-317
-
- Article
-
- You have access
- Export citation
Linear location estimators: the dependence of their quality on the shape of the probability density function, and their robustness
-
- Published online by Cambridge University Press:
- 17 April 2009, p. 319
-
- Article
-
- You have access
- Export citation
Front matter
BAZ volume 22 issue 2 Cover and Front matter
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back matter
BAZ volume 22 issue 2 Cover and Back matter
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation

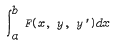 fails to possess a variational derivative, contrary to what is claimed by Gelfand and Fomin. A modified definition is given with respect to which the functional does possess a variational derivative.
fails to possess a variational derivative, contrary to what is claimed by Gelfand and Fomin. A modified definition is given with respect to which the functional does possess a variational derivative.