No CrossRef data available.
Article contents
On starlike functions
Published online by Cambridge University Press: 17 April 2009
Abstract
Let S denote the class of functions f analytic and univalent in the open disc {z: |z| < 1} and normalized by f(0) = 0 = f′(0) − 1, and S*(α) denote the set of starlike functions of order α (0 ≤ α ≤ 1) in S. In this paper, the results of William M. Causey and William L. White [J. Math. Anal. Appl. 64 (1978), 458–466] are generalized by the following:
THEOREM 1. Let f, g and h belong to S*(α), S*(λ) and S*(γ) , respectively and let F be defined by
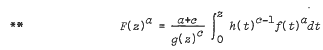
where a, c ∈ N. Then F belongs to S*(β) for |z| less than a suitably chosen number.
THEOREM 2. Let F, g and h belong to S*(α), S*(λ) and S*(γ) , respectively and f be given by **. Then f belongs to S*(β) , for |z| less than a suitably chosen number.
- Type
- Research Article
- Information
- Bulletin of the Australian Mathematical Society , Volume 22 , Issue 2 , October 1980 , pp. 241 - 247
- Copyright
- Copyright © Australian Mathematical Society 1980


