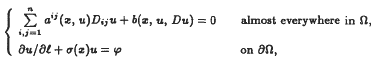Research Article
Derivations on semiprime rings
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 353-359
-
- Article
-
- You have access
- Export citation
A vanishing theorem for hyperplane cohomology
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 361-368
-
- Article
-
- You have access
- Export citation
For the minimal surface equation, the set of solvable boundary values need not be convex
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 369-372
-
- Article
-
- You have access
- Export citation
Global asymptotic stability of a periodic system of delay logistic equations
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 373-389
-
- Article
-
- You have access
- Export citation
Two characterisations of additive *-automorphisms of B(H)
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 391-400
-
- Article
-
- You have access
- Export citation
Homomorphisms of near-rings of continuous real-valued functions
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 401-411
-
- Article
-
- You have access
- Export citation
Duality map characterisations for Opial conditions
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 413-417
-
- Article
-
- You have access
- Export citation
Single identities for Mendelsohn and Steiner 3-quasigroups
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 419-424
-
- Article
-
- You have access
- Export citation
Commensurability and elementary equivalence of polycyclic groups
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 425-439
-
- Article
-
- You have access
- Export citation
On finite products of totally permutable groups
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 441-445
-
- Article
-
- You have access
- Export citation
Almost fixed point and best approximations theorems in H-spaces
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 447-454
-
- Article
-
- You have access
- Export citation
A characterisation of reflexive modules
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 455-458
-
- Article
-
- You have access
- Export citation
Remarks on bounded solutions of linear systems
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 459-467
-
- Article
-
- You have access
- Export citation
Width-diameter relations for planar convex sets with lattice point constraints
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 469-478
-
- Article
-
- You have access
- Export citation
A property of series of holomorphic homogeneous polynomials with Hadamard gaps
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 479-484
-
- Article
-
- You have access
- Export citation
Conditions for the solvability of singular boundary value problems
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 485-497
-
- Article
-
- You have access
- Export citation
On the cancellation problem of Zariski
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 499-500
-
- Article
-
- You have access
- Export citation
Oblique derivative problem for quasilinear elliptic equations with VMO coefficients
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 501-513
-
- Article
-
- You have access
- Export citation
On the behaviour of the sup- and inf-convolutions of a function near the boundary
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 515-520
-
- Article
-
- You have access
- Export citation
Abstracts of Australasian Ph.D. Theses
Combinatorial designs and related computational constructions
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 521-523
-
- Article
-
- You have access
- Export citation

 -residual, where
-residual, where  -projectors and
-projectors and 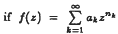 is a holomorphic function with Hadamard gaps on the open unit disc D then
is a holomorphic function with Hadamard gaps on the open unit disc D then 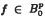 if and if only if
if and if only if 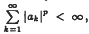 where
where 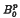 denote respectively the class of holomorphic functions on D which satisfy |
denote respectively the class of holomorphic functions on D which satisfy |