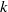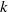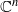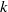Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Gao, Zhenghuan
Ma, Xinan
and
Zhang, Dekai
2023.
The exterior Dirichlet problem for the homogeneous complex k-Hessian equation.
Advanced Nonlinear Studies,
Vol. 23,
Issue. 1,