Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-11-27T16:01:35.578Z Has data issue: false hasContentIssue false
  • English
  • Français

Univalent functions with univalent Gelfond-Leontev derivatives

Published online by Cambridge University Press:  17 April 2009

O.P. Juneja  and
S.M. Shah
O.P. Juneja
Affiliation:
Department of Mathematics, Indian Institute of Technology, IIT Post Office, Kanpur 208016, U.P., India
S.M. Shah
Affiliation:
Department of Mathematics, University of Kentucky, Lexington, Kentucky 40506, USA.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 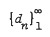be a nondecreasing sequence of positive numbers. We consider Gelfond-Leontev derivative Df(z), of a function 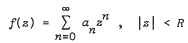, defined by 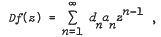for univalence and growth properties, and extend some results of Shah and Trimble. Set en = {d1d2 … dn), n≥l, e0 = 1, 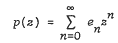. Let r be the radius of convergence of p(z). We state parts of Theorem 1 and Corollaries. Let f and all Dkf, k = 1, 2,…, be analytic and univalent in the unit disk U. Then

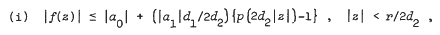
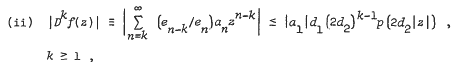
(iii) if p is entire and of growth (ρ, T) then f must be entire and of growth not exceeding (ρ, 2d2T),

(iv) if D corresponds to the shift operator (dn ≡ l), then .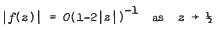

Another class of functions is defined by a condition of the form |an+1/an| ≤ bn+1/dn+1, where is a sequence of positive numbers satisfying and inequality, and it is shown that all functions in this class along with all their Gelfond–Leontev successive derivatives are regular and univalent in U. An extension of the definition of a linear invariant family is given and results analogous to (i) and (ii) are stated.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 29 , Issue 3 , June 1984 , pp. 329 - 348
Copyright
Copyright © Australian Mathematical Society 1984

References

[1]Boas, R.P., Entire functions (Academic Press, New York and London, 1954).Google Scholar
[2]Boas, R.P. and Buck, R.C., Polynomial expansions of analytic functions (Ergebnisse der Mathematik und ihrer Grenzgebiete, 19. Springer-Verlag, Berlin, Heidelberg, New York, 1964).CrossRefGoogle Scholar
[3]Buckholtz, J.D. and Frank, J.L., “Whittaker constants”, Proc. London Math. Soc. (3) 23 (1971), 248–270.Google Scholar
[4]Buckholtz, J.D. and Frank, J.L., “Whittaker constants – II”, J. Approx. Theory 10 (1974), 112–122.CrossRefGoogle Scholar
[5]Buckholtz, J.D. and Shah, S.M., “Analytic functions with constraints on coefficients”, J. Nonlinear Anal. 5 (1981), 553–564.CrossRefGoogle Scholar
[6]Campbell, D.M., “Locally univalent functions with locally univalent derivatives”, Trans. Amer. Math. Soc. 162 (1971), 395–409.CrossRefGoogle Scholar
[7]Gelfond, A.O. and Leontev, A.F., “On a generalization of Fourier series”, Mat. Sb. (N.S.) 29 (71), (1951), 477–500.Google Scholar
[8]Hayman, W.K., “Coefficient problems for univalent functions and related function classes”, J. London Math. Soc. 40 (1965), 305–406.Google Scholar
[9]Kazmin, Yu.A., “On an interpolation problem, I”, Sibirsk. Mat. ž. (1967), 293–312.Google Scholar
[70]Li, Chi-Mun, “The effect of the amplitudes of coefficients of holomorphis functions in the unit circle upon the schlichtness of the functions”, Chinese Math. Acta 5 (1964), 396–408.Google Scholar
[11]Nachbin, L., “An extension of the notion of integral functions of the finite exponential type”, Arias Acad. Brasil Ciencias 16 (1944), 143–147.Google Scholar
[12]Pommerenke, Ch., “Linear-invariante Familien Analytischer Funktionen, I”, Math. Ann. 155 (1964), 108–154.CrossRefGoogle Scholar
[13]Pommerenke, Ch., Univalent functions (Vandenhoeck and Ruprecht, Gottingen, 1975).Google Scholar
[14]Qin, Yuan-Xun, “On the arguments of the coefficients in the expansion of a univalent function”, Acta Math. Sinica 4 (1954), 81–86.Google Scholar
[15]Shah, S.M., “On the lower order of integral functions”, Bull. Amer. Math. Soc. 52 (1946), 1046–1052.CrossRefGoogle Scholar
[16]Shah, S.M., “On the coefficients of an entire series of finite order”, J. London Math. Soc. 26 (1951), 45–46.CrossRefGoogle Scholar
[17]Shah, S.M. and Trimble, S.Y., “Univalent functions with univalent derivatives”, Bull. Amer. Math. Soc. 75 (1969), 153–157.CrossRefGoogle Scholar
[18]Shah, S.M. and Trimble, S.Y., “Univalent functions with univalent derivatives, II”, Trans. Amer. Math. Soc. 144 (1969), 313–320.CrossRefGoogle Scholar
[19]Shah, S.M. and Trimble, S.Y., “Univalent functions with univalent derivatives, III”, J. Math. Mech. 19 (1969), 451–460.Google Scholar
[20]Shah, S.M. and Trimble, S.Y., “Univalence of derivatives of functions defined by gap power series”, J. London Math. Soc. (2) 9 (1975), 501–512.CrossRefGoogle Scholar
[21]Shah, S.M. and Trimble, S.Y., “Univalence of derivatives of functions defined by gap power series, II”, J. Math. Anal. Appl. 56 (1976), 28–40.CrossRefGoogle Scholar
[22]Shah, S.M. and Trimble, S.Y., “Analytic functions with univalent derivatives”, Indian J. Math. 20 (1978), 265–299.Google Scholar
[23]Srivastava, G.S. and Juneja, O.P., “The maximum term of a power series”, J. Math. Anal. Appl. 81 (1981), 1–7.CrossRefGoogle Scholar