Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-27T14:32:04.043Z Has data issue: false hasContentIssue false
  • English
  • Français

UNIVALENCE CRITERIA AND ANALOGUES OF THE JOHN CONSTANT

Part of: Geometric function theory

Published online by Cambridge University Press:  12 December 2012

YONG CHAN KIM  and
TOSHIYUKI SUGAWA
YONG CHAN KIM
Affiliation:
Department of Mathematics Education, Yeungnam University, 214-1 Daedong Gyongsan 712-749, Korea email [email protected]
TOSHIYUKI SUGAWA*
Affiliation:
Graduate School of Information Sciences, Tohoku University, Aoba-ku, Sendai 980-8579, Japan
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 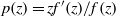$p(z)= z{f}^{\prime } (z)/ f(z)$ for a function 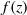$f(z)$ analytic on the unit disc 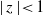$\mid z\mid \lt 1$ in the complex plane and normalised by 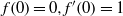$f(0)= 0, {f}^{\prime } (0)= 1$. We provide lower and upper bounds for the best constants 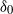${\delta }_{0} $ and 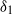${\delta }_{1} $ such that the conditions 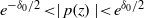${e}^{- {\delta }_{0} / 2} \lt \mid p(z)\mid \lt {e}^{{\delta }_{0} / 2} $ and 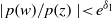$\mid p(w)/ p(z)\mid \lt {e}^{{\delta }_{1} } $ for 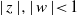$\mid z\mid , \mid w\mid \lt 1$ respectively imply univalence of 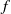$f$ on the unit disc.

Keywords

univalent functionunivalence criterionGrunsky coefficients

MSC classification

Secondary: 30C55: General theory of univalent and multivalent functions
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 88 , Issue 3 , December 2013 , pp. 423 - 434
Copyright
Copyright ©2012 Australian Mathematical Publishing Association Inc. 

References

Becker, J., ‘Löwnersche Differentialgleichung und quasikonform fortsetzbare schlichte Funktionen’, J. reine angew. Math. 255 (1972), 23–43.Google Scholar
Curtiss, J. H., ‘Polynomials and the Faber series’, Amer. Math. Monthly 78 (1971), 577–596.Google Scholar
Gevirtz, J., ‘An upper bound for the John constant’, Proc. Amer. Math. Soc. 83 (1981), 476–478.Google Scholar
Gevirtz, J., ‘On extremal functions for John constants’, J. Lond. Math. Soc. (2) 39 (1989), 285–298.Google Scholar
Hummel, J. A., ‘The Grunsky coefficients of a schlicht function’, Proc. Amer. Math. Soc. 15 (1964), 142–150.Google Scholar
Jabotinsky, E., ‘Universal relations between the elements of Grunsky’s matrix’, J. Anal. Math. 17 (1966), 411–417.Google Scholar
John, F., ‘On quasi-isometric mappings, II’, Comm. Pure Appl. Math. 22 (1969), 265–278.Google Scholar
Kim, Y. C., Ponnusamy, S. and Sugawa, T., ‘Mapping properties of nonlinear integral operators and pre-Schwarzian derivatives’, J. Math. Anal. Appl. 299 (2004), 433–447.Google Scholar
Kim, Y. C. and Sugawa, T., ‘On univalence of the power deformation $z\mathop{(f(z)/ z)}\nolimits ^{c} $’, Chinese Ann. Math. Ser. B. arXiv:1112.6237.Google Scholar
Pommerenke, Ch., Univalent Functions (Vandenhoeck & Ruprecht, Göttingen, 1975).Google Scholar
Todorov, P. G., ‘Three explicit formulas for the Taylor coefficients of the function $\mathop{(\frac{1- z}{1- xz} )}\nolimits ^{\lambda } $’, Abh. Math. Semin Univ. Hamb. 65 (1995), 147–153.Google Scholar
Yamashita, S., ‘On the John constant’, Math. Z. 161 (1978), 185–188.Google Scholar