Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-26T19:22:10.724Z Has data issue: false hasContentIssue false
  • English
  • Français

Topological and order-topological orthomodular lattices

Published online by Cambridge University Press:  17 April 2009

Zdenka Riecanová
Zdenka Riecanová
Affiliation:
Department of Mathematics Electrotechnical Faculty of the Slovak, Technical University, Ilkovicova 3 CS-812 19, Bratislava, Czechoslovakia
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The necessary and sufficient conditions for atomic orthomodular lattices to have the MacNeille completion modular, or (o)-continuous or order topological, orthomodular lattices are proved. Moreover we show that if in an orthomodular lattice the (o)-convergence of filters is topological then the (o)-convergence of nets need not be topological. Finally we show that even in the case when the MacNeille completion 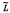of an orthomodular lattice L is order-topological, then in general the (o)-convergence of nets in 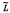does not imply their (o)-convergence in L. (This disproves, also for the orthomodular and order-topological case, one statement in G.Birkhoff's book.)

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 46 , Issue 3 , December 1992 , pp. 509 - 518
Copyright
Copyright © Australian Mathematical Society 1992

References

[1]Adams, D.H., ‘The completion by cuts of an orthocomplemented modular lattice’, Bull. Austral. Math. Soc. 1 (1969), 279–280.CrossRefGoogle Scholar
[2]Birkhoff, G., Lattice Theory (Providence, Rhode Island, 1967).Google Scholar
[3]Bruns, G., Greechie, R.J., Harding, J., and Roddy, M., ‘Completions of orthomodular lattices’, Order 7 (1990), 67–76.CrossRefGoogle Scholar
[4]Caászár, A., General topology (Akadémiai Kiadó, Budapest, 1978).Google Scholar
[5]Funayama, N., ‘On the completion by cuts of a distributive lattice’, Proc. Imp. Acad. Tokyo 20 (1944).Google Scholar
[6]Janowitz, M.F., ‘Indexed orthomodular lattices’, Math. Z. 119 (1971), 28–32.CrossRefGoogle Scholar
[7]Kalmbach, G., Orthomodular lattices (Academic Press, London, 1983).Google Scholar
[8]Kaplansky, J., ‘Any orthocomplemented complete modular lattice is continuous geometry’, Ann. of Math. 61 (1955), 524–541.CrossRefGoogle Scholar
[9]Kirchheimová, H., ‘Some remarks on (o)-convergence’, in Proc. of the First Winter School of Measure Theory, pp. 110–113 (Liptovský Ján, 1990).Google Scholar
[10]Erné, M., ‘Order-topological lattices’, Glasgow Math J. 21 (1980), 57–68.CrossRefGoogle Scholar
[11]Erné, M. and Weck, S., ‘Order convergence in lattices’, Rocky Mountain J. Math. 10 (1980), 805–818.CrossRefGoogle Scholar
[12]Pulmannová, S. and Riečanová, Z., ‘Compact topological orthomodular lattices’, in Contributions to General Algebra 7, pp. 277–282 (Verlag Hölder-Pichler-Tempsky, Wien, 1991).Google Scholar
[13]Riečanová, Z., ‘Topologies in atomic quantum logics’, Acta Univ. Carolin.—Math. Phys. 30, 143–148.Google Scholar
[14]Riečanová, Z., ‘Applications of topological methods to the completion of atomic orthomodular lattices’, Demonatratio Math. 24 (1991), 331–341.Google Scholar
[15]Schmidt, J., ‘Zur Kennzeichnung der Dedekind MacNeilleschen Hulle einer Geordneten Menge’, Arch. Math. 7 (1956), 241–249.CrossRefGoogle Scholar
[16]Choe, Tae Ho and Greechie, R.J., ‘Representation of locally compact orthomodular lattices’, (preprint).Google Scholar
[17]Choe, Tae Ho and Greechie, R.J., ‘Profinite orthomodular lattices’, (preprint).Google Scholar