Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-25T07:41:58.489Z Has data issue: false hasContentIssue false
  • English
  • Français

SOLVABILITY OF FINITE GROUPS WITH FOUR CONJUGACY CLASS SIZES OF CERTAIN ELEMENTS

Part of: Representation theory of groups Structure and classification of infinite or finite groups

Published online by Cambridge University Press:  21 July 2014

QINHUI JIANG  and
CHANGGUO SHAO
QINHUI JIANG
Affiliation:
School of Mathematical Sciences, University of Jinan, Shandong, 250022, PR China email [email protected]
CHANGGUO SHAO*
Affiliation:
School of Mathematical Sciences, University of Jinan, Shandong, 250022, PR China email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Assume that 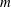$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}m$ and $n$ are two positive integers which do not divide each other. If the set of conjugacy class sizes of primary and biprimary elements of a group 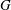$G$ is 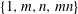$\{1, m, n, mn\}$, we show that up to central factors 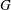$G$ is a 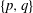$\{p,q\}$-group for two distinct primes 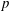$p$ and 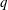$q$.

Keywords

conjugacy class sizesprimary and biprimary elementsfinite groups

MSC classification

Secondary: 20E45: Conjugacy classes 20D10: Solvable groups, theory of formations, Schunck classes, Fitting classes, $pi$-length, ranks
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 90 , Issue 2 , October 2014 , pp. 250 - 256
Copyright
Copyright © 2014 Australian Mathematical Publishing Association Inc. 

References

Alemany, E., Beltrán, A. and Felipe, M. J., ‘Finite groups with two p-regular conjugacy class lengths, II’, Bull. Aust. Math. Soc. 79 (2009), 419–425.CrossRefGoogle Scholar
Alemany, E., Beltrán, A. and Felipe, M. J., ‘Itô’s theorem on groups with two conjugacy class sizes revisited’, Bull. Aust. Math. Soc. 85 (2012), 476–481.CrossRefGoogle Scholar
Beltrán, A. and Felipe, M. J., ‘Variations on a theorem by Alan Camina on conjugacy class sizes’, J. Algebra 296 (2006), 253–266.CrossRefGoogle Scholar
Beltrán, A. and Felipe, M. J., ‘Some class size conditions implying solvability of finite groups’, J. Group Theory 9 (2006), 787–797.Google Scholar
Beltrán, A. and Felipe, M. J., ‘On the solvability of groups with four class sizes’, J. Algebra Appl. 11 (2012), 1250036-1.Google Scholar
Beltrán, A., Felipe, M. J. and Shao, C. G., Class sizes of prime-power order $p'$-elements and normal subgroups, Ann. Mat. Pura Appl. (4), to appear.Google Scholar
Camina, A. R., ‘Finite groups of conjugate rank 2’, Nagoya Math. J. 53 (1974), 47–57.Google Scholar
Kong, Q. and Guo, X., ‘On an extension of a theorem on conjugacy class sizes’, Israel J. Math. 179 (2010), 279–284.Google Scholar
Kong, Q. J. and Liu, Q. F., ‘Conjugacy class size conditions which imply solvability’, Bull. Aust. Math. Soc. 88 (2013), 297–300.Google Scholar
Kong, Q. J. and Liu, Q. F., ‘Correction to conjugacy class size conditions which imply solvability’, Bull. Aust. Math. Soc. 89 (2014), 522–523.Google Scholar
Kurzweil, H. and Stellmacher, B., The Theory of Finite Groups (Springer, New York, 2004).Google Scholar
Liu, X., Wang, Y. and Wei, H., ‘Notes on the length of conjugacy classes of finite groups’, J. Pure Appl. Algebra 196 (2005), 111–117.Google Scholar
Shao, C. G. and Jiang, Q. H., ‘On conjugacy class sizes of primary and biprimary elements of a finite group’, Sci. China Math. 57 (2014), 491–498.Google Scholar