Hostname: page-component-669899f699-tpknm Total loading time: 0 Render date: 2025-04-26T15:48:26.556Z Has data issue: false hasContentIssue false
  • English
  • Français

Smoothing spline in a convex closed set of Hilbert space

Published online by Cambridge University Press:  17 April 2009

Natasha Dicheva
Natasha Dicheva
Affiliation:
Department of Descriptive Geometry, University of Architecture, Civil Engineering and Geodesy, Boul. Hr. Smirnensky 1, Sofia 1421, Bulgaria e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A characterisation of a smoothing spline is sought in a convex closed set C of Hilbert space: 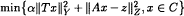, T and A are linear operators. A representation of the solution is obtained in the terms of the kernels of the above operators, of the dual operators T*, A* and of the dual cone C0. A particular case is considered when T is the differential operator and A is the operator-trace of a function.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 66 , Issue 3 , December 2002 , pp. 359 - 368
Copyright
Copyright © Australian Mathematical Society 2002

References

[1]Bojanov, B.D., Hakopian, H.A. and Sahakian, A.A., Spline functions and multivariate interpolations, Mathemtics and its Applications 248 (Kluwer Academic Publishers, Dordrecht, 1993).CrossRefGoogle Scholar
[2]le Cessie, S. and Balder, E.J., ‘A note on monotone interpolation and smoothing splines’, Numer. Funct. Anal. Optim. 15 (1994), 47–54.CrossRefGoogle Scholar
[3]Chui, C.K., Deutsch, F. and Ward, J., ‘Constrained best approximation in Hilbert space’, Constr. Approx. 6 (1990), 35–64.CrossRefGoogle Scholar
[4]Chui, C.K., Deutsch, F. and Ward, J., ‘Constrained best approximation in Hilbert space II’, J. Approx. Theory 71 (1992), 213–238.CrossRefGoogle Scholar
[5]Laurent, P.-J., Approximation et optimisation (Hermann, Paris, 1972).Google Scholar