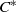Hostname: page-component-5cf477f64f-rdph2 Total loading time: 0 Render date: 2025-04-05T08:31:40.877Z Has data issue: false hasContentIssue false
  • English
  • Français

THE SIMILARITY DEGREE OF SOME ${C}^{\ast } $-ALGEBRAS

Part of: Methods of category theory in functional analysis Topological algebras, normed rings and algebras, Banach algebras Selfadjoint operator algebras Topological linear spaces and related structures General theory of linear operators

Published online by Cambridge University Press:  27 June 2013

DON HADWIN  and
WEIHUA LI
DON HADWIN*
Affiliation:
Department of Mathematics, University of New Hampshire, Durham, NH 03824, USA
WEIHUA LI
Affiliation:
Science and Mathematics Department, Columbia College Chicago, Chicago, IL 60605, USA email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We define the class of weakly approximately divisible unital 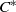${C}^{\ast } $-algebras and show that this class is closed under direct sums, direct limits, any tensor product with any 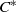${C}^{\ast } $-algebra, and quotients. A nuclear 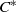${C}^{\ast } $-algebra is weakly approximately divisible if and only if it has no finite-dimensional representations. We also show that Pisier’s similarity degree of a weakly approximately divisible 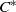${C}^{\ast } $-algebra is at most five.

Keywords

Kadison similarity problemsimilarity degreetracially nuclearC∗-algebra

MSC classification

Secondary: 46L05: General theory of $C^*$-algebras 46A22: Theorems of Hahn-Banach type; extension and lifting of functionals and operators 46H25: Normed modules and Banach modules, topological modules (if not placed in or ) 46M10: Projective and injective objects 47A20: Dilations, extensions, compressions
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 89 , Issue 1 , February 2014 , pp. 60 - 69
Copyright
Copyright ©2013 Australian Mathematical Publishing Association Inc. 

References

Blackadar, B., Kumjian, A. and Rørdam, M., ‘Approximately central matrix units and the structure of noncommutative tori’, K-Theory 6 (1992), 267–284.CrossRefGoogle Scholar
Bunce, J. W., ‘The similarity problem for representations of ${C}^{\ast } $-algebras’, Proc. Amer. Math. Soc. 81 (1981), 409–414.Google Scholar
Christensen, E., ‘On nonselfadjoint representations of ${C}^{\ast } $-algebras’, Amer. J. Math. 103 (1981), 817–833.CrossRefGoogle Scholar
Christensen, E., ‘Extensions of derivations II’, Math. Scand. 50 (1982), 111–122.CrossRefGoogle Scholar
Christensen, E., ‘Finite von Neumann algebra factors with property $\Gamma $’, J. Funct. Anal. 186 (2001), 366–380.CrossRefGoogle Scholar
Dixmier, J., ‘Étude sur les variétés et les opérateurs de Julia, avec quelques applications’, Bull. Soc. Math. France 77 (1949), 11–101.CrossRefGoogle Scholar
Foiaş, C., ‘Invariant para-closed subspaces’, Indiana Univ. Math. J. 21 (1971/72), 887–906.Google Scholar
Haagerup, U., ‘Solution of the similarity problem for cyclic representations of ${C}^{\ast } $-algebras’, Ann. Math. 118 (1983), 215–240.Google Scholar
Hadwin, D., ‘Dilations and Hahn decompositions for linear maps’, Canad. J. Math. 33 (1981), 826–839.Google Scholar
Hadwin, D. and Paulsen, V., ‘Two reformulations of Kadison’s similarity problem’, J. Operator Theory 55 (2006), 3–16.Google Scholar
Johanesová, M. and Winter, W., ‘The similarity problem for $ \mathcal{Z} $-stable ${C}^{\ast } $-algebras’, Bull. Lond. Math. Soc. 44 (6) (2012), 1215–1220.Google Scholar
Kadison, R., ‘On the orthogonalization of operator representations’, Amer. J. Math. 77 (1955), 600–622.CrossRefGoogle Scholar
Kirchberg, E., ‘The derivation problem and the similarity problem are equivalent’, J. Operator Theory 36 (1) (1996), 59–62.Google Scholar
Li, W., ‘The similarity degree of approximately divisible ${C}^{\ast } $-algebras’, Preprint, 2012, Oper. Matrices, to appear.CrossRefGoogle Scholar
Li, W. and Shen, J., ‘A note on approximately divisible ${C}^{\ast } $-algebras’, Preprint arXiv 0804.0465.Google Scholar
Paulsen, V. I., ‘Completely bounded maps on ${C}^{\ast } $-algebras and invariant operator ranges’, Proc. Amer. Math. Soc. 86 (1982), 91–96.Google Scholar
Paulsen, V. I., Completely Bounded Maps and Dilations, Pitman Research Notes in Mathematics Series, 146 (Longman Scientific & Technical, Harlow, 1986).Google Scholar
Pisier, G., ‘The similarity degree of an operator algebra’, Algebra i Analiz 10 (1998), 132–186; translation in St. Petersburg Math. J. 10 (1999), 103–146.Google Scholar
Pisier, G., ‘Remarks on the similarity degree of an operator algebra’, Internat. J. Math. 12 (2001), 403–414.Google Scholar
Pisier, G., ‘Similarity problems and length’, Taiwanese J. Math. 5 (2001), 1–17.Google Scholar
Pisier, G., Similarity Problems and Completely Bounded Maps, second, expanded edition. Lecture Notes in Mathematics, 1618 (Springer, Berlin, 2001).CrossRefGoogle Scholar
Pisier, G., ‘A similarity degree characterization of nuclear ${C}^{\ast } $-algebras’, Publ. Res. Inst. Math. Sci. 42 (3) (2006), 691–704.Google Scholar
Pop, F., ‘The similarity problem for tensor products of certain ${C}^{\ast } $-algebras’, Bull. Aust. Math. Soc. 70 (2004), 385–389.Google Scholar
Takesaki, M., Theory of Operator Algebras. I (Springer, New York, 1979).Google Scholar
Takesaki, M., ‘Nuclear ${C}^{\ast } $-algebras’, in: Theory of Operator Algebras. III, Encyclopaedia of Mathematical Sciences, 127 (Springer, Berlin, 2003), 153–204.Google Scholar
Wittstock, G., ‘Ein operatorwertiger Hahn-Banach Satz’, J. Funct. Anal. 40 (1981), 127–150.Google Scholar