Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Stavroulakis, I. P.
1989.
A note on a paper of Bowcock and Yu.
Bulletin of the Australian Mathematical Society,
Vol. 40,
Issue. 3,
p.
421.
Philos, Ch.G
1991.
Oscillations of first order linear retarded differential equations.
Journal of Mathematical Analysis and Applications,
Vol. 157,
Issue. 1,
p.
17.


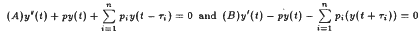 , where
, where 