Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-28T05:36:02.497Z Has data issue: false hasContentIssue false
  • English
  • Français

PRODUCTS OF ROTATIONS BY A GIVEN ANGLE IN THE ORTHOGONAL GROUP

Part of: Analytic and descriptive geometry Metric geometry Basic linear algebra

Published online by Cambridge University Press:  02 November 2017

M. G. MAHMOUDI Open the ORCID record for M. G. MAHMOUDI [Opens in a new window]
M. G. MAHMOUDI*
Affiliation:
Department of Mathematical Sciences, Sharif University of Technology, PO Box 11155-9415, Tehran, Iran email [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

For every rotation 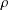$\unicode[STIX]{x1D70C}$ of the Euclidean space 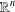$\mathbb{R}^{n}$ (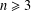$n\geq 3$), we find an upper bound for the number $r$ such that 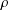$\unicode[STIX]{x1D70C}$ is a product of $r$ rotations by an angle $\unicode[STIX]{x1D6FC}$ (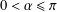$0<\unicode[STIX]{x1D6FC}\leq \unicode[STIX]{x1D70B}$). We also find an upper bound for the number $r$ such that 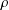$\unicode[STIX]{x1D70C}$ can be written as a product of $r$ full rotations by an angle $\unicode[STIX]{x1D6FC}$.

Keywords

rotation groupreflection

MSC classification

Primary: 51F25: Orthogonal and unitary groups
Secondary: 15A23: Factorization of matrices 51N30: Geometry of classical groups
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 97 , Issue 2 , April 2018 , pp. 308 - 312
Copyright
© 2017 Australian Mathematical Publishing Association Inc. 

References

Artin, E., Geometric Algebra (Interscience, New York, London, 1957).Google Scholar
Berger, M., Geometry I, Universitext (Springer, Berlin, 2009). (Translated from the 1977 French original by M. Cole and S. Levy; fourth printing of the 1987 English translation.)Google Scholar
Ellers, E. W., ‘Products of half-turns’, J. Algebra 99(2) (1986), 275–294.Google Scholar
Ellers, E. W. and Villa, O., ‘Half turns in characteristic 2’, Linear Algebra Appl. 483 (2015), 221–226.Google Scholar
Ishibashi, H., ‘On some systems of generators of the orthogonal groups’, Sci. Rep. Tokyo Kyoiku Daigaku Sect. A 11 (1972), 96–105.Google Scholar
Scherk, P., ‘On the decomposition of orthogonalities into symmetries’, Proc. Amer. Math. Soc. 1 (1950), 481–491.Google Scholar