POROSITY OF CERTAIN SUBSETS OF LEBESGUE SPACES ON LOCALLY COMPACT GROUPS

Abstract

Let 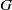$G$ be a locally compact group. In this paper, we show that if 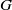$G$ is a nondiscrete locally compact group, 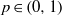$p\in (0, 1)$ and 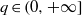$q\in (0, + \infty ] $, then 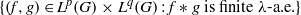$\{ (f, g)\in {L}^{p} (G)\times {L}^{q} (G): f\ast g\text{ is finite } \lambda \text{-a.e.} \} $ is a set of first category in 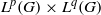${L}^{p} (G)\times {L}^{q} (G)$. We also show that if 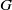$G$ is a nondiscrete locally compact group and 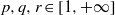$p, q, r\in [1, + \infty ] $ such that 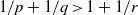$1/ p+ 1/ q\gt 1+ 1/ r$, then 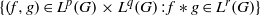$\{ (f, g)\in {L}^{p} (G)\times {L}^{q} (G): f\ast g\in {L}^{r} (G)\} $, is a set of first category in 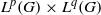${L}^{p} (G)\times {L}^{q} (G)$. Consequently, for 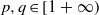$p, q\in [1+ \infty )$ and 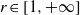$r\in [1, + \infty ] $ with 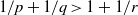$1/ p+ 1/ q\gt 1+ 1/ r$, 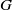$G$ is discrete if and only if 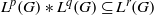${L}^{p} (G)\ast {L}^{q} (G)\subseteq {L}^{r} (G)$; this answers a question raised by Saeki [‘The 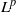${L}^{p} $-conjecture and Young’s inequality’, Illinois J. Math. 34 (1990), 615–627].