Hostname: page-component-6bf8c574d5-l72pf Total loading time: 0 Render date: 2025-03-04T11:01:59.803Z Has data issue: false hasContentIssue false
  • English
  • Français

PARTITIONS WITH AN ARBITRARY NUMBER OF SPECIFIED DISTANCES

Part of: Combinatorics Additive number theory; partitions

Published online by Cambridge University Press:  03 June 2019

BERNARD L. S. LIN Open the ORCID record for BERNARD L. S. LIN [Opens in a new window]
BERNARD L. S. LIN*
Affiliation:
School of Science, Jimei University, Xiamen 361021, PR China email [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

For positive integers 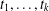$t_{1},\ldots ,t_{k}$, let 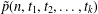$\tilde{p}(n,t_{1},t_{2},\ldots ,t_{k})$ (respectively 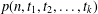$p(n,t_{1},t_{2},\ldots ,t_{k})$) be the number of partitions of $n$ such that, if 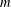$m$ is the smallest part, then each of 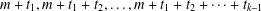$m+t_{1},m+t_{1}+t_{2},\ldots ,m+t_{1}+t_{2}+\cdots +t_{k-1}$ appears as a part and the largest part is at most (respectively equal to) 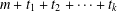$m+t_{1}+t_{2}+\cdots +t_{k}$. Andrews et al. [‘Partitions with fixed differences between largest and smallest parts’, Proc. Amer. Math. Soc.143 (2015), 4283–4289] found an explicit formula for the generating function of 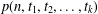$p(n,t_{1},t_{2},\ldots ,t_{k})$. We establish a 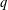$q$-series identity from which the formulae for the generating functions of 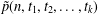$\tilde{p}(n,t_{1},t_{2},\ldots ,t_{k})$ and 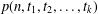$p(n,t_{1},t_{2},\ldots ,t_{k})$ can be obtained.

Keywords

partitiondifference between largest and smallest partsq-binomial theorem

MSC classification

Primary: 11P84: Partition identities; identities of Rogers-Ramanujan type
Secondary: 05A17: Partitions of integers
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 101 , Issue 1 , February 2020 , pp. 35 - 39
Copyright
© 2019 Australian Mathematical Publishing Association Inc. 

Footnotes

This work was supported by the National Natural Science Foundation of China (No. 11871246), the Natural Science Foundation of Fujian Province of China (No. 2019J01328) and the Program for New Century Excellent Talents in Fujian Province University (No. B17160).

References

Andrews, G. E., The Theory of Partitions (Addison-Wesley, New York, 1976).Google Scholar
Andrews, G. E., Beck, M. and Robbins, N., ‘Partitions with fixed differences between largest and smallest parts’, Proc. Amer. Math. Soc. 143 (2015), 4283–4289.Google Scholar
Breuer, F. and Kronholm, B., ‘A polyhedral model of partitions with bounded differences and a bijective proof of a theorem of Andrews, Beck, and Robbins’, Res. Number Theory 2 (2016), Article ID 2, 15 pages.10.1007/s40993-015-0033-3Google Scholar
Chapman, R., ‘Partitions with bounded differences between largest and smallest parts’, Australas. J. Combin. 64 (2016), 376–378.Google Scholar
Chern, S., ‘A curious identity and its applications to partitions with bounded part differences’, New Zealand J. Math. 47 (2017), 23–26.Google Scholar
Chern, S., ‘An overpartition analogue of partitions with bounded differences between largest and smallest parts’, Discrete Math. 340 (2017), 2834–2839.Google Scholar
Chern, S. and Yee, A. J., ‘Overpartitions with bounded part differences’, European J. Combin. 70 (2018), 317–324.Google Scholar