Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-27T02:31:56.963Z Has data issue: false hasContentIssue false
  • English
  • Français

ON THE DIFFERENCE OF COEFFICIENTS OF OZAKI CLOSE-TO-CONVEX FUNCTIONS

Part of: Geometric function theory

Published online by Cambridge University Press:  18 June 2020

YOUNG JAE SIM Open the ORCID record for YOUNG JAE SIM [Opens in a new window]  and
DEREK K. THOMAS Open the ORCID record for DEREK K. THOMAS [Opens in a new window]
YOUNG JAE SIM
Affiliation:
Department of Mathematics,Kyungsung University, Busan48434, Korea email [email protected]
DEREK K. THOMAS*
Affiliation:
Department of Mathematics,Swansea University, Bay Campus,Swansea, SA1 8EN, UK email [email protected]
*
✉[email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 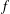$f$ be analytic in the unit disk 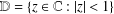$\mathbb{D}=\{z\in \mathbb{C}:|z|<1\}$ and 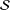${\mathcal{S}}$ be the subclass of normalised univalent functions given by 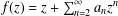$f(z)=z+\sum _{n=2}^{\infty }a_{n}z^{n}$ for 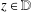$z\in \mathbb{D}$. We give sharp upper and lower bounds for $|a_{3}|-|a_{2}|$ and other related functionals for the subclass 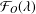${\mathcal{F}}_{O}(\unicode[STIX]{x1D706})$ of Ozaki close-to-convex functions.

Keywords

univalent functionOzaki close-to-convex functiondifference of coefficients

MSC classification

Primary: 30C50: Coefficient problems for univalent and multivalent functions
Secondary: 30C55: General theory of univalent and multivalent functions 30C45: Special classes of univalent and multivalent functions (starlike, convex, bounded rotation, etc.)
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 103 , Issue 1 , February 2021 , pp. 124 - 131
Check for updates
Copyright
© 2020 Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The first author was supported by a National Research Foundation of Korea (NRF) grant funded by the Korean Government (MSIP, Ministry of Science, ICT and Future Planning) (No. NRF-2017R1C1B5076778).

References

Allu, V., Tuneski, N. and Thomas, D. K., ‘On Ozaki close-to-convex functions’, Bull. Aust. Math. Soc. 99(1) (2019), 89–100.10.1017/S0004972718000989CrossRefGoogle Scholar
Arora, V., Ponnusamy, S. and Sahoo, S., ‘Successive coefficients for spirallike and related functions’, Rev. R. Acad. Cienc. Exactas Fís. Nat. Ser. A Mat. 113 (2019), 2969–2979.CrossRefGoogle Scholar
Cho, N. E., Kowalczyk, B. and Lecko, A., ‘Sharp bounds of some coefficient functionals over the class of functions convex in the direction of the imaginary axis’, Bull. Aust. Math. Soc. 100(1) (2019), 86–96.CrossRefGoogle Scholar
De Branges, L., ‘A proof of the Bieberbach conjecture’, Acta Math. 154(1–2) (1985), 137–152.CrossRefGoogle Scholar
Duren, P. L., Univalent Functions, Grundlehren der mathematischen Wissenschaften, 259 (Springer, New York, 1983).Google Scholar
Grinspan, A. Z., ‘The sharpening of the difference of the moduli of adjacent coefficients of schlicht functions’, in: Some Problems in Modern Function Theory, Proc. Conf. Modern Problems of Geometric Theory of Functions (Institute of Mathematics, Academy of Sciences of the USSR, Novosibirsk, 1976), 41–45. (in Russian).Google Scholar
Hayman, W. K., ‘On successive coefficients of univalent functions’, J. Lond. Math. Soc. 38 (1963), 228–243.CrossRefGoogle Scholar
Koepf, W., ‘On the Fekete–Szego problem for close to convex functions’, Proc. Amer. Math. Soc. 101 (1987), 89–95.Google Scholar
Leung, Y., ‘Successive coefficients of starlike functions’, Bull. Lond. Math. Soc. 10 (1978), 193–196.CrossRefGoogle Scholar
Ming, L. and Sugawa, T., ‘A note on successive coefficients of convex functions’, Comput. Methods Funct. Theory 17(2) (2017), 17900193.Google Scholar