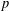Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Kerr, Bryce
Mello, Jorge
and
Shparlinski, Igor E.
2021.
On elements of large order on elliptic curves and multiplicative dependent images of rational functions over finite fields.
Illinois Journal of Mathematics,
Vol. 65,
Issue. 2,
Ghioca, Dragos
and
Shparlinski, Igor E.
2022.
Order of torsion for reduction of linearly independent points for a family of Drinfeld modules.
Journal of Number Theory,
Vol. 233,
Issue. ,
p.
112.