Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Nickolas, Peter
and
Tkachenko, Mikhail
2005.
The character of free topological groups I.
Applied General Topology,
Vol. 6,
Issue. 1,
p.
15.


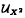 or the product uniformity u
or the product uniformity u