Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-26T07:20:53.607Z Has data issue: false hasContentIssue false
  • English
  • Français

ON COMPLEX HOMOGENEOUS SINGULARITIES

Part of: Singularities Cycles and subschemes (Co)homology theory Local theory

Published online by Cambridge University Press:  27 May 2019

QUY THUONG LÊ Open the ORCID record for QUY THUONG LÊ [Opens in a new window] ,
LAN PHU HOANG NGUYEN Open the ORCID record for LAN PHU HOANG NGUYEN [Opens in a new window]  and
DUC TAI PHO Open the ORCID record for DUC TAI PHO [Opens in a new window]
QUY THUONG LÊ*
Affiliation:
Department of Mathematics, Vietnam National University, Hanoi, 334 Nguyen Trai Street, Thanh Xuan District, Hanoi, Vietnam email [email protected]
LAN PHU HOANG NGUYEN
Affiliation:
Department of Mathematics, Vietnam National University, Hanoi, 334 Nguyen Trai Street, Thanh Xuan District, Hanoi, Vietnam email [email protected]
DUC TAI PHO
Affiliation:
Department of Mathematics, Vietnam National University, Hanoi, 334 Nguyen Trai Street, Thanh Xuan District, Hanoi, Vietnam email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We study the singularity at the origin of 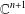$\mathbb{C}^{n+1}$ of an arbitrary homogeneous polynomial in 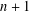$n+1$ variables with complex coefficients, by investigating the monodromy characteristic polynomials 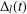$\unicode[STIX]{x1D6E5}_{l}(t)$ as well as the relation between the monodromy zeta function and the Hodge spectrum of the singularity. In the case 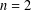$n=2$, we give a description of 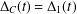$\unicode[STIX]{x1D6E5}_{C}(t)=\unicode[STIX]{x1D6E5}_{1}(t)$ in terms of the multiplier ideal.

Keywords

homogeneous singularitylog-resolutionlocal systemsmultiplier idealsfinite abelian coversHodge spectrumspectrum multiplicitymonodromy zeta function

MSC classification

Primary: 14B05: Singularities
Secondary: 14C20: Divisors, linear systems, invertible sheaves 14F18: Multiplier ideals 32S20: Global theory of singularities; cohomological properties
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 100 , Issue 3 , December 2019 , pp. 395 - 409
Copyright
© 2019 Australian Mathematical Publishing Association Inc. 

Footnotes

The first author’s research is funded by the Vietnam National Foundation for Science and Technology Development (NAFOSTED) under grant number FWO.101.2015.02; the third author’s research is funded by the Vietnam National University, Hanoi (VNU), under project number QG.15.02.

References

Abramovich, D. and Wang, J., ‘Equivariant resolution of singularities in characteristic 0’, Math. Res. Lett. 4(2–3) (1997), 427–433.Google Scholar
Budur, N., ‘On Hodge spectrum and multiplier ideals’, Math. Ann. 327(2) (2003), 257–270.Google Scholar
Budur, N., ‘Hodge spectrum of hyperplane arrangements’, Preprint, 2008, arXiv:0809.3443; incorporated in N. Budur and M. Saito, ‘Jumping coefficients and spectrum of a hyperplane arrangement’, Math. Ann. 347(3) (2010), 545–579.Google Scholar
Budur, N., ‘Unitary local systems, multiplier ideals, and polynomial periodicity of Hodge numbers’, Adv. Math. 221(1) (2009), 217–250.Google Scholar
Budur, N., Multiplier Ideals, Milnor Fibers, and Other Singularity Invariants, Lecture Notes, Luminy (2011), https://perswww.kuleuven.be/∼u0089821/LNLuminy.pdf.Google Scholar
Budur, N. and Saito, M., ‘Multiplier ideals, V-filtration, and spectrum’, J. Algebraic Geom. 14 (2005), 269–282.Google Scholar
Demailly, J. P., ‘A numerical criterion for very ample line bundles’, J. Differential Geom. 37(2) (1993), 323–374.Google Scholar
Denef, J. and Loeser, F., ‘Motivic Igusa zeta functions’, J. Algebraic Geom. 7 (1998), 505–537.Google Scholar
Dimca, A., Singularities and Topology of Hypersurfaces, Universitext (Springer, New York, 1992).Google Scholar
Ein, L. and Lazarsfeld, R., ‘Global generation of pluricanonical and adjoint linear series on smooth projective threefolds’, J. Amer. Math. Soc. 6(4) (1993), 875–903.Google Scholar
Esnault, H., ‘Fibre de Milnor d’un cône sur une courbe plane singulière’, Invent. Math. 68 (1982), 477–496.Google Scholar
Esnault, H. and Viehweg, E., Lectures on Vanishing Theorem, DMV Seminars, 68 (Birkhäuser, Basel, 1992).Google Scholar
Kollár, J., ‘Singularities of pairs’, in: Algebraic Geometry, Proceedings of Symposia in Pure Mathematics, 62, Part 1 (American Mathematical Society, Providence, RI, 1997), 221–287.Google Scholar
Lazarsfeld, R., Positivity in Algebraic Geometry II: Positivity for Vector Bundles, and Multiplier Ideals (Springer, Berlin, 2004).Google Scholar
Lê, D. T., ‘Some remarks on relative monodromy’, in: Real and Complex Singularities, Proc. Ninth Nordic Summer School/NAVF Sympos. Math., Oslo, August 5–25, 1976 (ed. Holm, P.) (Sijthoff and Noordhoff, Alphen aan den Rijn, 1977), 397–403.Google Scholar
Lê, Q. T., ‘Alexander polynomials of complex projective plane curves’, Bull. Aust. Math. Soc. 97 (2018), 386–395.Google Scholar
Libgober, A., ‘Alexander polynomial of plane algebraic curves and cyclic multiple planes’, Duke Math. J. 49 (1982), 833–851.Google Scholar
Libgober, A., ‘Alexander invariants of plane algebraic curves’, Proceedings of Symposia in Pure Mathematics, 40 (American Mathematcal Society, Providence, RI, 1983), 135–143.Google Scholar
Loeser, F. and Vaquié, M., ‘Le polynôme d’Alexander d’une courbe plane projective’, Topology 29 (1990), 163–173.Google Scholar
Milnor, J., Singular Points of Complex Hypersurfaces, Annals of Mathematics Studies, 61 (Princeton University Press, Princeton, NJ, 1968).Google Scholar
Milnor, J. and Orlik, P., ‘Isolated singularities defined by weighted homogeneous polynomials’, Topology 9 (1970), 385–393.Google Scholar
Nadel, A., ‘Multiplier ideal sheaves and Kähler–Einstein metrics of positive scalar curvature’, Ann. of Math. (2) 132(3) (1990), 549–596.Google Scholar
Saito, M., ‘Mixed Hodge modules and applications’, in: Proceedings of the ICM Kyoto, 1990 (ed. Satake, I.) (Springer, Tokyo, 1991), 725–734.Google Scholar
Steenbrink, J. H. M., ‘Mixed Hodge structure on the vanishing cohomology’, in: Real and Complex Singularities, Oslo 1976 (Sijthoff and Noordhoff, Alphen aan den Rijn, 1977), 525–563.Google Scholar
Steenbrink, J. H. M., ‘Intersection form for quasi-homogeneous singularities’, Compositio Math. 34 (1977), 211–223.Google Scholar