Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-28T20:17:00.692Z Has data issue: false hasContentIssue false
  • English
  • Français

ON A NONCRITICAL SYMMETRIC SQUARE 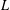$L$-VALUE OF THE CONGRUENT NUMBER ELLIPTIC CURVES

Part of: Arithmetic algebraic geometry

Published online by Cambridge University Press:  27 May 2019

DETCHAT SAMART Open the ORCID record for DETCHAT SAMART [Opens in a new window]
DETCHAT SAMART*
Affiliation:
Department of Mathematics, Burapha University, Chonburi, 20131, Thailand Center of Excellence in Mathematics, CHE, Bangkok, 10400, Thailand email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The congruent number elliptic curves are defined by 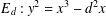$E_{d}:y^{2}=x^{3}-d^{2}x$, where 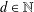$d\in \mathbb{N}$. We give a simple proof of a formula for 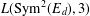$L(\operatorname{Sym}^{2}(E_{d}),3)$ in terms of the determinant of the elliptic trilogarithm evaluated at some degree zero divisors supported on the torsion points on 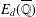$E_{d}(\overline{\mathbb{Q}})$.

Keywords

elliptic curvesymmetric square L-functionEisenstein–Kronecker serieselliptic polylogarithm

MSC classification

Primary: 11G40: $L$-functions of varieties over global fields; Birch-Swinnerton-Dyer conjecture
Secondary: 11G55: Polylogarithms and relations with $K$-theory
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 101 , Issue 1 , February 2020 , pp. 13 - 22
Copyright
© 2019 Australian Mathematical Publishing Association Inc. 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bloch, S., Higher Regulators, Algebraic K-theory, and Zeta Functions of Elliptic Curves, CRM Monograph Series, 11 (American Mathematical Society, Providence, RI, 2000).Google Scholar
Coates, J. and Schmidt, C. G., ‘Iwasawa theory for the symmetric square of an elliptic curve’, J. reine angew. Math. 375/376 (1987), 104–156.Google Scholar
Goncharov, A. B., ‘Mixed elliptic motives’, in: Galois Representations in Arithmetic Algebraic Geometry, London Mathematical Society Lecture Note Series, 243 (Cambridge University Press, Cambridge, 1998), 147–221.10.1017/CBO9780511662010.005Google Scholar
Goncharov, A. and Levin, A., ‘Zagier’s conjecture on L (E, 2)’, Invent. Math. 132 (1998), 393–432.10.1007/s002220050228Google Scholar
Glasser, M. L. and Zucker, I. J., ‘Lattice sums’, in: Theoretical Chemistry—Advances and Perspectives. V (Academic Press, New York, 1980), 67–139.Google Scholar
Koblitz, N., Introduction to Elliptic Curves and Modular Forms (Springer, New York, 1993).10.1007/978-1-4612-0909-6Google Scholar
Mestre, J. and Schappacher, N., ‘Séries de Kronecker et fonctions L des puissances symétriques de courbes elliptiques sur ℚ’, in: Arithmetic Algebraic Geometry, Progress in Mathematics, 89 (Birkhäuser, Boston, MA, 1991), 209–245.10.1007/978-1-4612-0457-2_10Google Scholar
Ono, K., The Web of Modularity: Arithmetic of the Coefficients of Modular Forms and q-Series, CBMS Regional Conference Series in Mathematics, 102 (American Mathematical Society, Providence, RI, 2004).Google Scholar
Samart, D., ‘The elliptic trilogarithm and Mahler measures of K3 surfaces’, Forum Math. 28 (2016), 405–423.10.1515/forum-2014-0045Google Scholar
Samart, D., ‘Three-variable Mahler measures and special values of modular and Dirichlet L-series’, Ramanujan J. 32 (2013), 245–268.10.1007/s11139-013-9464-4Google Scholar
Wildeshaus, J., ‘On an elliptic analogue of Zagier’s conjecture’, Duke Math. J. 87 (1997), 355–407.10.1215/S0012-7094-97-08714-7Google Scholar
Zagier, D., ‘The Bloch–Wigner–Ramakrishnan polylogarithm function’, Math. Ann. 286 (1990), 613–624.10.1007/BF01453591Google Scholar
Zagier, D. and Gangl, H., ‘Classical and elliptic polylogarithms and special values of L-series’, in: The Arithmetic and Geometry of Algebraic Cycles, Proceedings, 1998 CRM Summer School, Nato Science Series C, 548 (Kluwer, Dordrecht, 2000), 561–615.Google Scholar