Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-27T02:11:56.335Z Has data issue: false hasContentIssue false
  • English
  • Français

NUMERICAL RANGE AND POSITIVE BLOCK MATRICES

Part of: Basic linear algebra General theory of linear operators

Published online by Cambridge University Press:  11 June 2020

JEAN-CHRISTOPHE BOURIN  and
EUN-YOUNG LEE
JEAN-CHRISTOPHE BOURIN
Affiliation:
Laboratoire de Mathématiques de Besançon, UMR 6623, CNRS, Université de Bourgogne Franche-Comté, Besançon, France email [email protected]
EUN-YOUNG LEE*
Affiliation:
Department of Mathematics, KNU-Center for Nonlinear Dynamics, Kyungpook National University, Daegu 702-701, Korea email [email protected]
*
✉[email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We obtain several norm and eigenvalue inequalities for positive matrices partitioned into four blocks. The results involve the numerical range 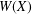$W(X)$ of the off-diagonal block 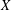$X$, especially the distance 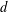$d$ from 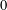$0$ to 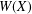$W(X)$. A special consequence is an estimate,

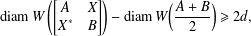$$\begin{eqnarray}\text{diam}\,W\left(\left[\begin{array}{@{}cc@{}}A & X\\ X^{\ast } & B\end{array}\right]\right)-\text{diam}\,W\biggl(\frac{A+B}{2}\biggr)\geq 2d,\end{eqnarray}$$
between the diameters of the numerical ranges for the full matrix and its partial trace.

Keywords

numerical rangepartitioned matricesnorm inequalities

MSC classification

Primary: 15A60: Norms of matrices, numerical range, applications of functional analysis to matrix theory
Secondary: 15A42: Inequalities involving eigenvalues and eigenvectors 47A12: Numerical range, numerical radius 47A30: Norms (inequalities, more than one norm, etc.)
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 103 , Issue 1 , February 2021 , pp. 69 - 77
Check for updates
Copyright
© 2020 Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The first author was funded by the ANR Project No. ANR-19-CE40-0002 and by the French Investissements d’Avenir program, project ISITE-BFC (contract ANR-15-IDEX-03). The second author was supported by the Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Education (NRF-2018R1D1A3B07043682).

References

Ando, T., ‘Majorization, doubly stochastic matrices, and comparison of eigenvalues’, Linear Algebra Appl. 118 (1989), 163–248.CrossRefGoogle Scholar
Bhatia, R., Matrix Analysis, Graduate Texts in Mathematics, 169 (Springer, New York, 1996).Google Scholar
Bourin, J.-C. and Hiai, F., ‘Norm and anti-norm inequalities for positive semi-definite matrices’, Int. J. Math. 22 (2011), 1121–1138.CrossRefGoogle Scholar
Bourin, J.-C. and Hiai, F., ‘Jensen and Minkowski inequalities for operator means and anti-norms’, Linear Algebra Appl. 456 (2014), 22–53.CrossRefGoogle Scholar
Bourin, J.-C. and Lee, E.-Y., ‘Decomposition and partial trace of positive matrices with Hermitian blocks’, Int. J. Math. 24 (2013), 1350010.CrossRefGoogle Scholar
Bourin, J.-C., Lee, E.-Y. and Lin, M., ‘Positive matrices partitioned into a small number of Hermitian blocks’, Linear Algebra Appl. 438 (2013), 2591–2598.CrossRefGoogle Scholar
Bourin, J.-C. and Mhanna, A., ‘Positive block matrices and numerical ranges’, C. R. Acad. Sci. Paris 355(10) (2017), 1077–1081.CrossRefGoogle Scholar
Cain, B. E., ‘Improved inequalities for the numerical radius: when inverse commutes with the norm’, Bull. Aust. Math. Soc. 97(2) (2018), 293–296.CrossRefGoogle Scholar
Gumus, M., Liu, J., Raouafi, S. and Tam, T.-Y., ‘Positive semi-definite 2 × 2 block matrices and norm inequalities’, Linear Algebra Appl. 551 (2018), 83–91.CrossRefGoogle Scholar
Hayashi, T., ‘On a norm inequality for a positive block-matrix’, Linear Algebra Appl. 566 (2019), 86–97.CrossRefGoogle Scholar
Holbrook, J. A. R., ‘Multiplicative properties of the numerical radius in operator theory’, J. reine angew. Math. 237 (1969), 166–174.Google Scholar
Horn, R. and Johnson, C. R., Topics in Matrix Analysis (Cambridge University Press, Cambridge, 1994), corrected reprint of the 1991 original.Google Scholar
Kittaneh, F., ‘Numerical radius inequalities for Hilbert space operators’, Studia Math. 168(1) (2005), 73–80.CrossRefGoogle Scholar
Mhanna, A., ‘On symmetric norm inequalities and positive definite block-matrices’, Math. Inequal. Appl. 21(1) (2018), 133–138.Google Scholar
Simon, B., Trace Ideals and Their Applications, 2nd edn, Mathematical Surveys and Monographs, 120 (American Mathematical Society, Providence, RI, 2005).Google Scholar