Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-23T21:29:57.659Z Has data issue: false hasContentIssue false
  • English
  • Français

A NOTE ON THE ERDŐS–GRAHAM THEOREM

Part of: Sequences and sets

Published online by Cambridge University Press:  23 April 2018

WENHUI WANG  and
MIN TANG
WENHUI WANG
Affiliation:
School of Mathematics and Computer Science, Anhui Normal University, Wuhu 241003, China email [email protected]
MIN TANG*
Affiliation:
School of Mathematics and Computer Science, Anhui Normal University, Wuhu 241003, China email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 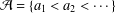${\mathcal{A}}=\{a_{1}<a_{2}<\cdots \,\}$ be a set of nonnegative integers. Put 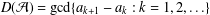$D({\mathcal{A}})=\gcd \{a_{k+1}-a_{k}:k=1,2,\ldots \}$. The set 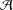${\mathcal{A}}$ is an asymptotic basis if there exists 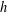$h$ such that every sufficiently large integer is a sum of at most 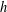$h$ (not necessarily distinct) elements of 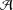${\mathcal{A}}$. We prove that if the difference of consecutive integers of 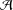${\mathcal{A}}$ is bounded, then 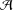${\mathcal{A}}$ is an asymptotic basis if and only if there exists an integer 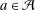$a\in {\mathcal{A}}$ such that 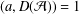$(a,D({\mathcal{A}}))=1$.

Keywords

asymptotic basisexact order

MSC classification

Primary: 11B13: Additive bases, including sumsets
Secondary: 11B50: Sequences (mod $m$)
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 97 , Issue 3 , June 2018 , pp. 363 - 366
Copyright
© 2018 Australian Mathematical Publishing Association Inc. 

Footnotes

This work was supported by the National Natural Science Foundation of China (Grant No.11471017).

References

Chen, S. and Gu, W. Z., ‘Exact order of subsets of asymptotic bases’, J. Number Theory 41 (1992), 15–21.CrossRefGoogle Scholar
Erdős, P. and Graham, R. L., ‘On bases with an exact order’, Acta Arith. 37 (1980), 201–207.CrossRefGoogle Scholar
Jia, X. D., ‘Exact order of subsets of asympotic bases in additive number theory’, J. Number Theory 28 (1988), 205–218.Google Scholar
Nash, J. C. M. and Nathanson, M. B., ‘Cofinite subsets of asymptotic bases for the positive integers’, J. Number Theory 20 (1985), 363–372.CrossRefGoogle Scholar
Nathanson, M. B., ‘The exact order of subsets of additive bases’, in: Number Theory (New York, 1982), Lecture Notes in Mathematics, 1052 (Springer, Berlin, 1984), 273–277.Google Scholar
Plagne, A., ‘Removing one element from an exact additive basis’, J. Number Theory 87 (2001), 306–314.CrossRefGoogle Scholar
Yang, Q. H. and Chen, F. J., ‘On bases with a T-order’, Integers 11 (2011), A5.CrossRefGoogle Scholar