Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Galewska, Elżbieta
and
Galewski, Marek
2006.
On the stability of solutions for thep(x)-Laplacian equation and some applications to optimisation problems with state constraints.
The ANZIAM Journal,
Vol. 48,
Issue. 2,
p.
245.
Galewski, Marek
and
Plócienniczak, Marek
2007.
On Existence and Stability of Solutions to Elliptic Systems with Generalised Growth.
Bulletin of the Australian Mathematical Society,
Vol. 76,
Issue. 3,
p.
453.
Galewski, Marek
and
Płócienniczak, Marek
2007.
On the Nonlinear Dirichlet Problem withP(x)-Laplacian.
Bulletin of the Australian Mathematical Society,
Vol. 75,
Issue. 3,
p.
381.
Galewski, Marek
2007.
On the existence and stability of solutions for Dirichlet problem withp(x)-Laplacian.
Journal of Mathematical Analysis and Applications,
Vol. 326,
Issue. 1,
p.
352.
Galewski, Marek
2007.
On a Dirichlet Problem with Generalizedp(x)-Laplacian and Some Applications.
Numerical Functional Analysis and Optimization,
Vol. 28,
Issue. 9-10,
p.
1087.
Galewski, Marek
2008.
On a Dirichlet problem with p(x)-Laplacian.
Journal of Mathematical Analysis and Applications,
Vol. 337,
Issue. 1,
p.
281.
Dai, Guowei
and
Liu, Wulong
2009.
Three solutions for a differential inclusion problem involving the -Laplacian.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 71,
Issue. 11,
p.
5318.
Dai, Guowei
2009.
Infinitely many non-negative solutions for a Dirichlet problem involving -Laplacian.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 71,
Issue. 11,
p.
5840.
Dai, Guowei
2009.
Infinitely many solutions for a differential inclusion problem in involving the -Laplacian.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 71,
Issue. 3-4,
p.
1116.
Dai, Guowei
2009.
Infinitely many solutions for a Neumann-type differential inclusion problem involving the p (x )-Laplacian.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 70,
Issue. 6,
p.
2297.
Dai, Guowei
2009.
Three solutions for a Neumann-type differential inclusion problem involving the p(x)-Laplacian.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 70,
Issue. 10,
p.
3755.
Yongqiang, Fu
and
Mei, Yu
2010.
Existence of Solutions for the -Laplacian Problem with Singular Term.
Boundary Value Problems,
Vol. 2010,
Issue. 1,
p.
584843.
Fu, Yongqiang
and
Yu, Mei
2010.
The Dirichlet problem of higher order quasilinear elliptic equation.
Journal of Mathematical Analysis and Applications,
Vol. 363,
Issue. 2,
p.
679.
Fu, Yongqiang
and
Yu, Mei
2010.
The Neumann boundary value problem of higher order quasilinear elliptic equation.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 72,
Issue. 12,
p.
4488.
Mei, Yu
Yongqiang, Fu
Wang, Li
and
Hirano, Norimichi
2012.
Existence of Solutions for the p(x)‐Laplacian Problem with the Critical Sobolev‐Hardy Exponent.
Abstract and Applied Analysis,
Vol. 2012,
Issue. 1,
Fu, Yongqiang
and
Yang, Miaomiao
2014.
Nonlocal Variational Principles with Variable Growth.
Journal of Function Spaces,
Vol. 2014,
Issue. ,
p.
1.
Fu, Yongqiang
and
Yang, Miaomiao
2014.
Existence of solutions for quasilinear elliptic systems in divergence form with variable growth.
Journal of Inequalities and Applications,
Vol. 2014,
Issue. 1,
Vélin, J.
2016.
Existence result for a gradient-type elliptic system involving a pair ofp(x) andq(x)-Laplacian operators.
Complex Variables and Elliptic Equations,
Vol. 61,
Issue. 5,
p.
644.
Avci, Mustafa
and
Süer, Berat
2019.
On a nonlocal problem involving a nonstandard nonhomogeneous differential operator.
Journal of Elliptic and Parabolic Equations,
Vol. 5,
Issue. 1,
p.
47.


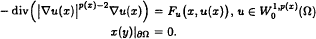 without assuming Palais-Smale condition.
without assuming Palais-Smale condition.