Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-26T08:46:37.030Z Has data issue: false hasContentIssue false
  • English
  • Français

A NEW UPPER BOUND FOR THE SUM OF DIVISORS FUNCTION

Part of: Elementary number theory Computational number theory

Published online by Cambridge University Press:  14 August 2017

CHRISTIAN AXLER Open the ORCID record for CHRISTIAN AXLER [Opens in a new window]
CHRISTIAN AXLER*
Affiliation:
Institute of Mathematics, Heinrich Heine University, Duesseldorf, 40225 Duesseldorf, Germany email [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Robin’s criterion states that the Riemann hypothesis is true if and only if 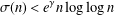$\unicode[STIX]{x1D70E}(n)<e^{\unicode[STIX]{x1D6FE}}n\log \log n$ for every positive integer 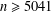$n\geq 5041$. In this paper we establish a new unconditional upper bound for the sum of divisors function, which improves the current best unconditional estimate given by Robin. For this purpose, we use a precise approximation for Chebyshev’s $\unicode[STIX]{x1D717}$-function.

Keywords

Riemann hypothesisRobin’s inequalitysum of divisors function

MSC classification

Primary: 11A25: Arithmetic functions; related numbers; inversion formulas
Secondary: 11Y70: Values of arithmetic functions; tables
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 96 , Issue 3 , December 2017 , pp. 374 - 379
Copyright
© 2017 Australian Mathematical Publishing Association Inc. 

References

Akbary, A., Friggstad, Z. and Juricevic, R., ‘Explicit upper bounds for ∏ p≤p 𝜔(n) p/(p - 1)’, Contrib. Discrete Math. 2(2) (2007), 153–160.Google Scholar
Alaoglu, L. and Erdős, P., ‘On highly composite and similar numbers’, Trans. Amer. Math. Soc. 56 (1944), 448–469.Google Scholar
Axler, C., ‘New estimates for some prime functions’, Preprint, 2017, available at arXiv:1703.08032.Google Scholar
Banks, W. D., Hart, D. N., Moree, P., Nevans, C. W. and Wesley, C., ‘The Nicolas and Robin inequalities with sums of two squares’, Monatsh. Math. 157(4) (2009), 303–322.Google Scholar
Briggs, K., ‘Abundant numbers and the Riemann hypothesis’, Exp. Math. 15(2) (2006), 251–256.CrossRefGoogle Scholar
Broughan, K. and Trudgian, T., ‘Robin’s inequality for 11-free integers’, Integers 15 (2015), Article ID A12, 5 pages.Google Scholar
Choie, Y.-J., Lichiardopol, N., Moree, P. and Solé, P., ‘On Robin’s criterion for the Riemann hypothesis’, J. Théor. Nombres Bordeaux 19(2) (2007), 357–372.Google Scholar
Dusart, P., ‘Explicit estimates of some functions over primes’, Ramanujan J. (2016), doi:10.1007/s11139-016-9839-4.Google Scholar
Gronwall, T. H., ‘Some asymptotic expressions in the theory of numbers’, Trans. Amer. Math. Soc. 14(1) (1913), 113–122.Google Scholar
Grytczuk, A., ‘Upper bound for sum of divisors function and the Riemann hypothesis’, Tsukuba J. Math. 31(1) (2007), 67–75.Google Scholar
Hertlein, A., ‘Robin’s inequality for new families of integers’, Preprint, 2016, available at arXiv:1612.05186.Google Scholar
Ivić, A., ‘Two inequalities for the sum of divisors functions’, Univ. u Novom Sadu Zb. Rad. Prirod.-Mat. Fak. 7 (1977), 17–22.Google Scholar
Mertens, F., ‘Ein Beitrag zur analytischen Zahlentheorie’, J. reine angew. Math. 78 (1874), 42–62.Google Scholar
Ramanujan, S., ‘Highly composite numbers, annotated and with a foreword by Nicolas and Robin’, Ramanujan J. 1(2) (1997), 119–153.Google Scholar
Robin, G., ‘Grandes valeurs de la fonction somme des diviseurs et hypothèse de Riemann’, J. Math. Pures Appl. 63(2) (1984), 187–213.Google Scholar
Solé, P. and Planat, M., ‘The Robin inequality for 7-free integers’, Integers 12(2) (2012), 301–309.Google Scholar