Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-28T18:15:45.489Z Has data issue: false hasContentIssue false
  • English
  • Français

THE NATURAL PARTIAL ORDER ON SOME TRANSFORMATION SEMIGROUPS

Part of: Ordered sets Semigroups

Published online by Cambridge University Press:  28 June 2013

SUREEPORN CHAOPRAKNOI ,
TEERAPHONG PHONGPATTANACHAROEN  and
PATTANACHAI RAWIWAN
SUREEPORN CHAOPRAKNOI*
Affiliation:
Department of Mathematics and Computer Science, Faculty of Science, Chulalongkorn University, Bangkok 10330, Thailand email [email protected][email protected]
TEERAPHONG PHONGPATTANACHAROEN
Affiliation:
Department of Mathematics and Computer Science, Faculty of Science, Chulalongkorn University, Bangkok 10330, Thailand email [email protected][email protected]
PATTANACHAI RAWIWAN
Affiliation:
Department of Mathematics and Computer Science, Faculty of Science, Chulalongkorn University, Bangkok 10330, Thailand email [email protected][email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

For a semigroup 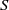$S$, let 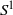${S}^{1} $ be the semigroup obtained from 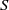$S$ by adding a new symbol 1 as its identity if 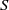$S$ has no identity; otherwise let 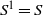${S}^{1} = S$. Mitsch defined the natural partial order 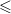$\leqslant $ on a semigroup 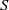$S$ as follows: for 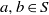$a, b\in S$, 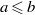$a\leqslant b$ if and only if 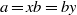$a= xb= by$ and 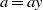$a= ay$ for some 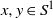$x, y\in {S}^{1} $. In this paper, we characterise the natural partial order on some transformation semigroups. In these partially ordered sets, we determine the compatibility of their elements, and find all minimal and maximal elements.

Keywords

transformation semigroupsnatural partial orderleft (right) compatibleminimal (maximal) elements

MSC classification

Secondary: 20M20: Semigroups of transformations, etc. 06A06: Partial order, general
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 89 , Issue 2 , April 2014 , pp. 279 - 292
Copyright
Copyright ©2013 Australian Mathematical Publishing Association Inc. 

References

Hartwig, R., ‘How to partially order regular elements’, Math. Japon. 25 (1980), 1–13.Google Scholar
Higgins, P. M., ‘The Mitsch order on a semigroup’, Semigroup Forum 49 (1994), 261–266.Google Scholar
Kemprasit, Y., Algebraic Semigroup Theory (Pitak Press, Bangkok, 2002).Google Scholar
Kowol, G. and Mitsch, H., ‘Naturally ordered transformation semigroups’, Monatsh. Math. 102 (1986), 115–138.Google Scholar
Marques-Smith, M. P. O. and Sullivan, R. P., ‘Partial orders on transformation semigroups’, Monatsh. Math. 140 (2003), 103–118.CrossRefGoogle Scholar
Mitsch, H., ‘A natural partial order for semigroups’, Proc. Amer. Math. Soc. 97 (1986), 384–388.Google Scholar
Nambooripad, K., ‘The natural partial order on a regular semigroup’, Proc. Edinb. Math. Soc. 23 (1980), 249–260.Google Scholar
Noknoi, R., Generalized Transformation Semigroup Admitting Hyperring Structure (Master’s Thesis, Chulalongkorn University, 1981).Google Scholar
Wagner, V., ‘Generalized groups’, Dokl. Akad. Nauk SSSR 84 (1952), 1119–1122; (in Russian).Google Scholar