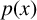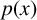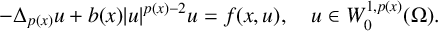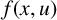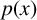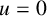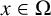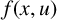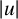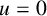MULTIPLE SOLUTIONS FOR $p(x)$-LAPLACIAN EQUATIONS WITH NONLINEARITY SUBLINEAR AT ZERO

Abstract

We consider the Dirichlet problem for $p(x)$-Laplacian equations of the form

$$ \begin{align*} -\Delta_{p(x)}u+b(x)\vert u\vert ^{p(x)-2}u=f(x,u),\quad u\in W_{0}^{1,p(x)}(\Omega). \end{align*} $$

The odd nonlinearity $f(x,u)$ is $p(x)$-sublinear at $u=0$ but the related limit need not be uniform for $x\in \Omega $. Except being subcritical, no additional assumption is imposed on $f(x,u)$ for $|u|$ large. By applying Clark’s theorem and a truncation method, we obtain a sequence of solutions with negative energy and approaching the zero function $u=0$.

1 Introduction

Let $\Omega \subset \mathbb {R}^{N}$ be a bounded smooth domain, $p:\overline {\Omega }\rightarrow \mathbb {R}$ be Lipschitz continuous and

(1.1) $$ \begin{align} 1<p_{-}:=\inf_{x\in\Omega}p(x)\leq\sup_{x\in\Omega}p(x)=:p_{+}<N\text{.} \end{align} $$

We consider the Dirichlet problem for the $p(x)$ -Laplacian equation

(1.2) $$ \begin{align} \bigg\{\!\!\! \begin{array} [c]{r@{}ll} -\Delta_{p(x)}u+b(x)\vert u\vert^{p(x)-2} &u=f(x,u) & \text{in } \Omega ,\\ &u=0\ \qquad & \text{on } \partial\Omega, \end{array} \end{align} $$

where $\Delta _{p(x)}u=\operatorname {div}( \vert \nabla u\vert ^{p(x)-2}\nabla u) $ is the $p(x)$ -Laplacian of u and $b\in L^{N/p(x)} (\Omega )$ . The definition of the space $L^{N/p(x)} (\Omega )$ is given in the next section. Note that b can be sign-changing. Let

$$ \begin{align*} p^{\ast}(x)=\frac{Np(x)}{N-p(x)}. \end{align*} $$

We assume the following conditions on the nonlinearity $f(x,u)$ :

1. (f ₁) $f:\Omega \times \mathbb {R}\rightarrow \mathbb {R}$ satisfies the Carathéodory condition and

   $$ \begin{align*} \vert f(x,t)\vert \leq C_{1}+C_{2}\vert t\vert ^{q(x)-1}\quad \mbox{for all}\ (x,t) \in\Omega\times \mathbb{R}\text{,} \end{align*} $$
   where $q\in C(\overline {\Omega })$ and $1< q(x)<p^{*}(x)$ for all $x\in \Omega $ ;

2. (f ₂) there is a ball $B_{r}(a)\subset \Omega $ such that

   (1.3) $$ \begin{align} \lim_{\vert t\vert \rightarrow0}\frac{F(x,t)}{\vert t\vert ^{p_{-}}}=+\infty\quad\text{ for almost every (a.e.) }x\in B_{r} (a)\text{, where }F(x,t)=\int_{0}^{t}f(x,\cdot)\text{.} \end{align} $$

When $p(x)\equiv 2$ (thus $p_{-}=2$ ) and $f(x,\cdot )$ is sublinear at zero, then (1.3) holds with $p_{-}=2$ . For this reason, we say that our problem (1.2) is $p(x)$ -sublinear at zero. We emphasise that the limit (1.3) is a pointwise limit, while condition $( f_{1}) $ means that the nonlinearity $f(x,u)$ is subcritical. Under these mild conditions, we shall prove the following theorem.

Theorem 1.1. Suppose that the conditions $( f_{1}) $ and $( f_{2}) $ hold. If $f(x,\cdot )$ is odd for all $x\in \Omega $ , then (1.2) has a sequence of solutions $u_{n}$ such that $\Phi (u_{n})\leq 0$ , $\Phi (u_{n})\rightarrow 0$ ; where $\Phi $ is the energy functional given in (3.1).

This theorem generalises a recent result of He and Wu [5], where the semilinear case $p(x)\equiv 2$ , namely

(1.4) $$ \begin{align} \bigg\{\!\!\! \begin{array} [c]{r@{}ll} -\Delta u+b(x)&u=f(x,u) & \text{in}\ \Omega,\\ &u=0\ \qquad & \text{on}\ \partial\Omega, \end{array} \end{align} $$

is considered assuming $b\in L^{N/2}(\Omega )$ and $f(x,u)$ is subcritical. In particular, He and Wu assumed the pointwise limit

(1.5) $$ \begin{align} \lim_{\vert t\vert \rightarrow0}\frac{F(x,t)}{\vert t\vert ^{2}}=+\infty\quad\text{ for }x\in\Omega\text{.} \end{align} $$

However, in their argument, to verify the condition (1.6) in Proposition 1.2 below, they need the inequality

$$ \begin{align*} F(x,t)\geq c_{k}^{-2}\vert t\vert ^{2}\qquad\text{ for }\vert t\vert \leq r\text{ and a.e. }x\in\Omega\text{.} \end{align*} $$

This could not be true unless the limit (1.5) holds uniformly. In the proof of our Theorem 1.1, we fill this gap (see Lemma 3.4) and generalise their result to the quasilinear variable exponent case. Moreover, the verification of the $(PS)_{c}$ condition, which is crucial for applying variational methods, has been greatly simplified (see Remark 3.3).

Both [5] and our result are based on a new version of Clark’s theorem recently proved by Liu and Wang [8]. Our Theorem 1.1 is motivated by [5].

Proposition 1.2 [8, Theorem 1.1].

Let W be a Banach space and $\Phi \in C^{1}(W,\mathbb {R})$ be an even coercive functional satisfying the $( PS) _{c}$ condition for $c\leq 0$ and $\Phi (0)=0$ . If for any $k\in \mathbb {N}$ there are a k-dimensional subspace $W_{k}$ and $\delta _{k}>0$ such that

(1.6) $$ \begin{align} \sup_{W_{k}\cap S_{\delta_{k}}}\Phi<0\text{,} \end{align} $$

where $S_{r}=\{ u\in W : \Vert u\Vert =r\} $ for $r>0$ , then $\Phi $ has a sequence of critical points $u_{k}\neq 0$ such that $\Phi (u_{k})\leq 0$ , $u_{k}\rightarrow 0$ .

Variable exponent variational problems appear in many applications (see [2, 6, 9]). In particular, there has been great interest in elliptic boundary value problems involving the $p(x)$ -Laplacian in the last two decades. In [7], a sequence of negative energy solutions of the $p(x)$ -Laplacian equation in (1.2) subject to a nonlinear boundary condition is obtained; in addition to $(f_{1})$ and $(f_{2})$ , it is assumed that (1.3) holds uniformly for $x\in \Omega $ and that the nonlinearity is $p(x)$ -sublinear at infinity. In [10], the existence of positive solutions of (1.2) with concave and convex nonlinearities is studied via Nehari’s method. For other recent results, we refer to [11] for $p(x)$ -Laplacian systems and to [1] for $(p(x),q(x))$ -Laplacian problems.

2 Variable exponent spaces

To study the problem (1.2), we recall the variable exponent Lebesgue space and Sobolev space (see [4] for more details). For a Lipschitz continuous function ${p:\overline {\Omega }\rightarrow \mathbb {R}}$ satisfying (1.1), let

$$ \begin{align*} L^{p(x)}(\Omega)=\bigg\{ u:\Omega\rightarrow\mathbb{R} : u\text{ is measurable and }\int\vert u\vert ^{p(x)}<\infty \bigg\} \text{.} \end{align*} $$

Here and below, all integrals are taken over $\Omega $ . Equipped with the Luxemburg norm,

$$ \begin{align*} \vert u\vert _{p(x)}=\inf\bigg\{ \lambda>0 : \int\bigg\vert \frac{u}{\lambda}\bigg\vert ^{p(x)}\leq1 \bigg\} \text{,} \end{align*} $$

$L^{p(x)}(\Omega )$ becomes a separable uniformly convex Banach space.

The variable exponent Sobolev space $W_{0}^{1,p(x)}(\Omega )$ is the completion of $C_{0}^{\infty }(\Omega )$ under the norm

$$ \begin{align*} \Vert u\Vert =\vert \nabla u\vert _{p(x)}=\inf\bigg\{ \lambda>0 : \int\bigg\vert \frac{\nabla u}{\lambda}\bigg\vert ^{p(x)}\leq1 \bigg\} \text{,} \end{align*} $$

which is also a separable uniformly convex Banach space.

From now on, we denote $W=W_{0}^{1,p(x)}(\Omega )$ . The functional $\rho :W\rightarrow \mathbb {R}$ defined by

$$ \begin{align*} \rho(u)=\int\frac{1}{p(x)}\vert \nabla u\vert ^{p(x)} \end{align*} $$

is crucial for investigating $p(x)$ -Laplacian equations like (1.2).

Lemma 2.1 [3, Theorem 3.1].

The functional $\rho $ is of class $C^{1}$ . Moreover, the functional $\rho ^{\prime }:W\rightarrow W^{\ast }$ is of type $( S_{+}) $ . Thus, if $u_{n}\rightharpoonup u$ in W and

$$ \begin{align*} \varlimsup_{n\rightarrow\infty}\langle\rho^{\prime}(u_{n}),u_{n}-u\rangle \leq0\text{,} \end{align*} $$

then $u_{n}\rightarrow u$ in W.

From the definition of the norm $\|\cdot \|$ , it is easy to see that:

1. (1) if $\Vert u\Vert \geq 1$ , then

   $$ \begin{align*} \Vert u\Vert ^{p_{-}}\leq\int\vert \nabla u\vert ^{p(x)}\leq\Vert u\Vert ^{p_{+}}\text{;} \end{align*} $$

2. (2) if $\Vert u\Vert \leq 1$ , then

   $$ \begin{align*} \Vert u\Vert ^{p_{+}}\leq\int\vert \nabla u\vert ^{p(x)}\leq\Vert u\Vert ^{p_{-}}\text{.} \end{align*} $$

The following lemma is an easy consequence because $p_{-}\le p(x)\le p_{+}$ .

Lemma 2.2

1. (1) If $\Vert u\Vert \geq 1$ , then

   $$ \begin{align*} \frac{1}{p_{+}}\Vert u\Vert ^{p_{-}}\leq\rho(u)\leq\frac{1}{p_{-} }\Vert u\Vert ^{p_{+}}\text{;} \end{align*} $$

2. (2) if $\Vert u\Vert \leq 1$ , then

   $$ \begin{align*} \frac{1}{p_{+}}\Vert u\Vert ^{p_{+}}\leq\rho(u)\leq\frac{1}{p_{-} }\Vert u\Vert ^{p_{-}}\text{.} \end{align*} $$

3 Proof of Theorem 1.1

For the variable exponent Sobolev space $W=W_{0}^{1,p(x)} (\Omega )$ , it is well known that weak solutions of (1.2) are precisely critical points of the $C^{1}$ -functional $\Phi :W\rightarrow \mathbb {R}$ ,

(3.1) $$ \begin{align} \Phi(u)=\int\bigg( \frac{1}{p(x)}( \vert \nabla u\vert ^{p(x)}+b(x)\vert u\vert ^{p(x)}) \bigg) -\int F(x,u)\text{.} \end{align} $$

At first glance, because b may be sign-changing, the principle part (the first term) of $\Phi $ appears to be indefinite. We observe that if we set

$$ \begin{align*} \tilde{f}(x,t)=f(x,t)-b(x)\vert t\vert ^{p(x)-2}t\text{,} \end{align*} $$

then the problem (1.2) becomes

$$ \begin{align*} \bigg\{\!\!\! \begin{array} [c]{r@{}ll} -\Delta_{p(x)}&u=\tilde{f}(x,u) & \text{in}\ \Omega,\\ &u=0\ \qquad & \text{on}\ \partial\Omega, \end{array} \end{align*} $$

in which the new nonlinearity $\tilde {f}(x,u)$ satisfies the same conditions $( f_{1}) $ and $( f_{2}) $ , and

$$ \begin{align*} \lim_{\vert t\vert \rightarrow0}\frac{\tilde{F}(x,t)}{\vert t\vert ^{p_{-}}}=\lim_{\vert t\vert \rightarrow0}\bigg( \frac{F(x,t)}{\vert t\vert ^{p_{-}}}-\frac{b(x)}{p(x)} \frac{\vert t\vert ^{p(x)}}{\vert t\vert ^{p_{-}} }\bigg) =\lim_{\vert t\vert \rightarrow0}\frac{F(x,t)}{\vert t\vert ^{p_{-}}}=+\infty \end{align*} $$

for almost every $x\in B_{r}(a)$ , because $p(x)\geq p_{-}$ . Here, $\tilde {F}(x,t)=\int _{0}^{t}\tilde {f}(x,\cdot )$ .

In other words, to prove Theorem 1.1, it suffices to consider the case $b(x)=0$ . The reason that we state our problem (1.2) with the term $b(x)\vert u\vert ^{p(x)-2}u$ is to allow comparison with the results of [5, 7, 10].

Therefore, in what follows, we assume $b(x)=0$ so that the functional given in (3.1) becomes $\Phi :W\rightarrow \mathbb {R}$ ,

$$ \begin{align*} \Phi(u) =\rho(u)-\int F(x,u) =\int\frac{1}{p(x)}\vert \nabla u\vert ^{p(x)}-\int F(x,u)\text{,} \end{align*} $$

whose critical points are solutions of (1.2) with $b(x)=0$ . To prove Theorem 1.1, we shall apply Proposition 1.2 to find a sequence $\{ u_{n}\} $ of critical points for $\Phi $ .

Since we have not assumed any conditions on the nonlinearity $f(x,t)$ for $|t|$ large (except the subcritical growth condition $( f_{1}) $ ), it is not possible to verify the $( PS) _{c}$ condition for $\Phi $ . To overcome this difficulty, we adopt the truncation method of He and Wu [5].

Let $\phi :[0,\infty )\rightarrow \lbrack 0,1]$ be a decreasing $C^{\infty } $ -function such that $\vert \phi ^{\prime }(t)\vert \leq 2$ ,

$$ \begin{align*} \phi(t)=1\text{ for }t\in[ 0,1] \quad \text{and} \quad \phi(t)=0\text{ for }t\in\lbrack2,\infty)\text{.} \end{align*} $$

We consider the truncated functional $\Psi :W\rightarrow \mathbb {R}$ ,

$$ \begin{align*} \Psi(u)=\rho(u)-\phi(\rho(u))\int F(x,u)\text{.} \end{align*} $$

The derivative of $\Psi $ is given by

(3.2) $$ \begin{align} \langle\Psi^{\prime}(u),v\rangle & =\langle\rho^{\prime}(u),v\rangle -\phi(\rho(u))\int f(x,u)v-\bigg( \int F(x,u)\bigg) \phi^{\prime} (\rho(u))\langle\rho^{\prime}(u),v\rangle\nonumber\\ & =\bigg( 1-\bigg( \int F(x,u)\bigg) \phi^{\prime}(\rho(u))\bigg) \langle\rho^{\prime}(u),v\rangle-\phi(\rho(u))\int f(x,u)v \end{align} $$

for $u,v\in W$ .

Lemma 3.1. The functional $\Psi $ is coercive.

Proof. We note that by Lemma 2.2, for $\Vert u\Vert \geq 1+( 2p_{+}) ^{1/p_{-}}$ ,

$$ \begin{align*} \rho(u)\geq\frac{1}{p_{+}}\Vert u\Vert ^{p_{-}}\geq2\text{.} \end{align*} $$

Hence, $\phi (\rho (u))=0$ and

$$ \begin{align*} \Psi(u)=\rho(u)\geq\frac{1}{p_{+}}\Vert u\Vert ^{p_{-}}\text{.} \end{align*} $$

This implies that $\Psi $ is coercive.

Lemma 3.2. The functional $\Psi $ satisfies $( PS) _{c}$ for $c\leq 0$ .

Proof. Let $\{ u_{n}\} $ be a $( PS) _{c}$ sequence of $\Psi $ with $c\leq 0$ , that is, $\Psi (u_{n})\rightarrow c$ , $\Psi ^{\prime } (u_{n})\rightarrow 0$ . Then for n large,

(3.3) $$ \begin{align} -\phi(\rho(u_{n}))\int F(x,u_{n})=\Psi(u_{n})-\rho(u_{n})\leq\frac{1}{2} -\rho(u_{n})\text{.} \end{align} $$

We claim that

(3.4) $$ \begin{align} 1-\bigg( \int F(x,u_{n})\bigg) \phi^{\prime}(\rho(u_{n}))\geq 1\text{.} \end{align} $$

For this purpose, we consider two cases. If $\rho (u_{n})<1$ , then $\phi ^{\prime }(\rho (u_{n}))=0$ and (3.4) is an equality. If $\rho (u_{n})\geq 1$ , then the right-hand side of (3.3) is negative. Noting $\phi (\rho (u_{n}))\geq 0$ , we have

(3.5) $$ \begin{align} \int F(x,u_{n})\geq0\text{.} \end{align} $$

So we also have (3.4) because $\phi ^{\prime }(\rho (u_{n}))\leq 0$ .

The coerciveness of $\Psi $ implies that the $( PS) _{c}$ sequence $\{ u_{n}\} $ is bounded in W. We may assume that $u_{n}\rightharpoonup u$ in W. Since f is subcritical (condition $(f_{1} )$ ), by the compact embedding $W\hookrightarrow L^{q(x)}(\Omega )$ , Hölder’s inequality and the boundedness of the Nemytsky operator

$$ \begin{align*} \mathcal{N}_{f}:L^{q(x)}(\Omega)\rightarrow L^{q(x)/(q(x)-1)}(\Omega )\text{,}\quad(\mathcal{N}_{f}u)(x)=f(x,u(x))\text{,} \end{align*} $$

(as shown in [4]), it is well known that up to a subsequence,

(3.6) $$ \begin{align} \bigg\vert\! \int f(x,u_{n})( u_{n}-u) \bigg\vert \leq 2|f(x,u_{n})|_{q(x)/(q(x)-1)}|u_{n}-u|_{q(x)}\rightarrow0\text{.} \end{align} $$

Setting $v=u_{n}-u$ in (3.2), from $\langle \Psi ^{\prime }(u_{n} ),u_{n}-u\rangle \rightarrow 0$ , (3.6) and the boundedness of $\phi (\rho (u_{n}))$ , we obtain

(3.7) $$ \begin{align} \bigg( 1 & -\bigg( \int F(x,u_{n})\bigg) \phi^{\prime} (\rho(u_{n}))\bigg) \langle\rho^{\prime}(u_{n}),u_{n}-u\rangle\nonumber\\ & =\langle\Psi^{\prime}(u_{n}),u_{n}-u\rangle+\phi(\rho(u_{n}))\int f(x,u_{n})( u_{n}-u) \rightarrow0\text{.} \end{align} $$

We deduce from this and (3.4) that

$$ \begin{align*} \langle\rho^{\prime}(u_{n}),u_{n}-u\rangle\rightarrow0\text{.} \end{align*} $$

It follows from Lemma 2.1 that $u_{n}\rightarrow u$ in W.

Remark 3.3. Although our problem (1.2) is much more general than the problem (1.4) considered in [5], our verification of the $( PS) _{c}$ condition is much simpler than in [5], where the convergence of $\{u_{n}\}$ is deduced by estimating $\Vert u_{n}-u\Vert ^{2}$ by the sum of $\langle \Psi ^{\prime }(u_{n})-\Psi ^{\prime }(u),u_{n}-u\rangle $ and four additional complicated terms (see [5, (2.20)]). The key points in our proof are the $(S_{+})$ property of $\rho ^{\prime }$ and the observation (3.4).

We should also point out that the verification of $(PS)_c$ for $c=0$ in [5] contains a gap. For the $(PS)_0$ sequence $\{u_n\}$ , [5, (2.19)] is derived from ${2\Psi (u_n)-\|u_n\|^2\le 0}$ . However, this may be false because $\Psi (u_n)$ may be positive, even though $\Psi (u_n)\to 0$ .

Lemma 3.4. For any $k\in \mathbb {N}$ , there are a k-dimensional subspace $W_{k}$ of W and $\delta _{k}>0$ , such that

$$ \begin{align*} \sup_{W_{k}\cap S_{\delta_{k}}}\Psi<0\text{.} \end{align*} $$

Proof. Let $X=\{u\in W : \operatorname {\mathrm {supp}} u\subset B_{r}(a)\}$ , $W_{k}$ be a k-dimensional subspace of X. If the result is not true then, for all $n\in \mathbb {N}$ ,

$$ \begin{align*} \sup_{W_{k}\cap S_{1/n}}\Psi\geq0\text{.} \end{align*} $$

This implies that there is a sequence $\{ u_{n}\} \subset W_{k}\cap S_{1/n}$ , such that

(3.8) $$ \begin{align} \|u_{n}\|=\frac1n\to0\text{,}\quad\Psi(u_{n})\geq-\frac{1}{n^{p_{-}}}\text{.} \end{align} $$

Since all norms on $W_{k}$ are equivalent, from $\Vert u_{n}\Vert \rightarrow 0$ , we deduce $\vert u_{n}\vert _{\infty }\rightarrow 0$ .

Let $\eta :\Omega \rightarrow [ -\infty ,\infty ] $ be defined by

$$ \begin{align*} \eta(x)=\varliminf_{n\rightarrow\infty}\frac{F(x,u_{n}(x))}{\Vert u_{n}\Vert ^{p_{-}}}\text{.} \end{align*} $$

Then $\eta $ is measurable. For $x\in B_{r}(a)$ , from the pointwise limit (1.3) in $( f_{2}) $ , there is $r_{x}>0$ such that $F(x,t)\geq 0$ for $t\in [ -r_{x},r_{x}] $ . Hence, if $n\gg 1$ , then $\vert u_{n}\vert _{\infty }\leq r_{x}$ and $F(x,u_{n}(x))\geq 0$ , and so $\eta (x)\ge 0$ for a.e. $x\in B_{r}(a)$ . Consequently, $\eta (x)\geq 0$ for a.e. $x\in \Omega $ , because $\operatorname {\mathrm {supp}} u_{n}\subset B_{r}(a)$ .

Let $v_{n}=\Vert u_{n}\Vert ^{-1}u_{n}$ . Since $\dim W_{k}<\infty $ , we have $v_{n}\rightarrow v$ in $W_{k}$ for some $v\in W_{k}$ , note that $\|v\|=1$ . For $x\in \{ v\neq 0\} $ , using (1.3) again,

$$ \begin{align*} \eta(x)=\varliminf_{n\rightarrow\infty}\frac{F(x,u_{n}(x))}{\Vert u_{n}\Vert ^{p_{-}}}=\varliminf_{n\rightarrow\infty}\frac{F(x,u_{n} (x))}{\vert u_{n}(x)\vert ^{p_{-}}}\vert v_{n}(x)\vert ^{p_{-}}=+\infty\text{.} \end{align*} $$

By Fatou’s lemma, since $\{ v\neq 0\} $ has positive Lebesgue measure,

(3.9) $$ \begin{align} \varliminf_{n\rightarrow\infty}\int\frac{F(x,u_{n})}{\Vert u_{n} \Vert ^{p_{-}}}\geq\int\varliminf_{n\rightarrow\infty}\frac{F(x,u_{n} )}{\Vert u_{n}\Vert ^{p_{-}}}=\int\eta\geq\int_{v\neq0}\eta =+\infty\text{.} \end{align} $$

Because $\Vert u_{n}\Vert \leq 1$ , we have (see Lemma 2.2)

$$ \begin{align*} \rho(u_{n})\leq\frac{1}{p_{-}}\Vert u_{n}\Vert ^{p_{-}} \leq1\text{.} \end{align*} $$

Thus, $\phi (\rho (u_{n}))=1$ and

$$ \begin{align*} \Psi(u_{n}) =\Phi(u_{n}) & =\rho(u_{n})-\int F(x,u_{n})\\ & \leq\frac{1}{p_{-}}\Vert u_{n}\Vert ^{p_{-}}-\int F(x,u_{n})\\ & =\Vert u_{n}\Vert ^{p_{-}}\bigg( \frac{1}{p_{-}}-\int \frac{F(x,u_{n})}{\Vert u_{n}\Vert ^{p_{-}}}\bigg) =\frac {1}{n^{p_{-}}}\bigg( \frac{1}{p_{-}}-\int\frac{F(x,u_{n})}{\Vert u_{n}\Vert ^{p_{-}}}\bigg) \text{.} \end{align*} $$

Now, from (3.9), we deduce $n^{p_{-}}\Psi (u_{n})\rightarrow -\infty $ , contradicting (3.8).

Proof of Theorem 1.1.

Lemmas 3.1, 3.2 and 3.4 permit us to apply Proposition 1.2, and deduce that $\Psi $ has a sequence of critical points $u_{k}\neq 0$ such that $\Psi (u_{k})<0$ and $u_{k}\rightarrow 0$ in W. For some $K\in \mathbb {N}$ , if $k\geq K$ ,

$$ \begin{align*} \rho(u_{k})\leq\frac{1}{p_{-}}\Vert u_{k}\Vert ^{p_{-}}<1\text{.} \end{align*} $$

Since $\Psi (u)=\Phi (u)$ for $u\in \rho ^{-1}[0,1)$ , we see that $u_{k}$ with $k\geq K$ are critical points of $\Phi $ as well, satisfying $\Phi (u_{k})<0$ and $u_{k}\rightarrow 0$ in W.

Remark 3.5. Liu and Wang [8, Theorem 3.1] treat the case in which $p(x)$ is a constant $p>1$ . Assuming that $f(x,\cdot )$ is odd only in $( -\delta ,\delta ) $ for some $\delta>0$ , and

(3.10) $$ \begin{align} \lim_{\vert t\vert \rightarrow0}\frac{F(x,t)}{\vert t\vert ^{p}}=+\infty \end{align} $$

uniformly on some small ball $B_{r}(x_{0})\subset \Omega $ , a sequence of negative energy solutions approaching zero is obtained. Liu and Wang truncated the nonlinearity $f(x,t)$ for $\vert t\vert>\delta /2$ , resulting in a new nonlinearity $\hat {f}(x,t)=0$ for $\vert t\vert>\delta $ . Then Proposition 1.2 is applied to get a sequence of solutions $u_{n}$ for the truncated problem. Since $u_{n}\rightarrow 0$ in $W_{0}^{1,p}(\Omega )$ , a regularity argument then yields $\vert u_{n}\vert _{\infty }<\delta /2$ for large n. Such $u_{n}$ are then solutions of the original problem.

To the best of our knowledge, a suitable $L^{\infty }$ -regularity theory is not available for the $p(x)$ -Laplacian operator and, at present, we can only deal with the case in which $f(x,\cdot )$ is globally odd and subcritical, as we have done in Theorem 1.1. Our argument in proving Lemma 3.4 can be used to slightly improve [8, Theorem 3.1], requiring only that the limit (3.10) holds pointwise in $B_{r}(x_{0})$ .