Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-23T19:21:17.307Z Has data issue: false hasContentIssue false
  • English
  • Français

Monochromatic solutions to equations with unit fractions

Published online by Cambridge University Press:  17 April 2009

Tom C. Brown  and
Voijtech Rödl
Tom C. Brown
Affiliation:
Department of Mathematics and Statistics, Simon Fraser University, Burnaby BC, CanadaV5A 1S6
Voijtech Rödl
Affiliation:
Department of Mathematics and Computer Science, Emory University, Atlanta GA 30322-9998, United States of America
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Our main result is that if G(x1, …, xn) = 0 is a system of homogeneous equations such that for every partition of the positive integers into finitely many classes there are distinct y1,…, yn in one class such that G(y1, …, yn) = 0, then, for every partition of the positive integers into finitely many classes there are distinct Z1, …, Zn in one class such that

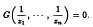
In particular, we show that if the positive integers are split into r classes, then for every n ≥ 2 there are distinct positive integers x1, x1, …, xn in one class such that

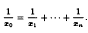
We also show that if [1, n6 − (n2 − n)2] is partitioned into two classes, then some class contains x0, x1, …, xn such that

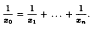
(Here, x0, x2, …, xn are not necessarily distinct.)

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 43 , Issue 3 , June 1991 , pp. 387 - 392
Copyright
Copyright © Australian Mathematical Society 1991

References

[1]Erdös, P. and Graham, R.L., Old and new problems and results in combinatorial number theory, L’enseignement mathematique (Universite de Geneve, Geneva, 1980).Google Scholar
[2]Graham, R.L., Rothschild, B.L. and Spencer, J.H., Ramsey theory (John Wiley and Sons, New York, 1980).Google Scholar
[3]Rado, R., ‘Studien zur Kombinatorik’, Math. Z. 36 (1933), 424–480.CrossRefGoogle Scholar