Article contents
Local analytic structure in certain commutative topological algebras
Published online by Cambridge University Press: 17 April 2009
Abstract
Let B be a topological algebra with Fréchet space topology, A an algebra with locally convex topology and 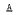 an algebra of formal power series over A in n commuting indeterminates which carries a Fréchet space topology. In a previous paper the author showed, for the case n = 1, that a homomorphism of B into
an algebra of formal power series over A in n commuting indeterminates which carries a Fréchet space topology. In a previous paper the author showed, for the case n = 1, that a homomorphism of B into  whose range contains polynomials is necessarily continuous provided the coordinate projections of
whose range contains polynomials is necessarily continuous provided the coordinate projections of 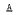 into A satisfy a certain equicontinuity condition. This result is here extended to the case of general n, and also to weaker topological assumptions.
into A satisfy a certain equicontinuity condition. This result is here extended to the case of general n, and also to weaker topological assumptions.
- Type
- Research Article
- Information
- Copyright
- Copyright © Australian Mathematical Society 1972
References
- 5
- Cited by


