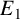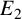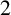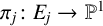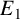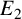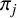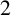1 Introduction
For an elliptic curve E over
![]() $\mathbb {C}$
, we let
$\mathbb {C}$
, we let
![]() $E[\infty ]$
be the set of all its torsion points. A morphism
$E[\infty ]$
be the set of all its torsion points. A morphism
![]() $f\colon E\to {\mathbb {P}}^1$
is said to be even if
$f\colon E\to {\mathbb {P}}^1$
is said to be even if
![]() $f(-P)=f(P)$
for all P in E. In 2007, Bogomolov and Tschinkel [Reference Bogomolov, Tschinkel and Zannier3] used Raynaud’s theorem (the Manin–Mumford conjecture) to prove the following result.
$f(-P)=f(P)$
for all P in E. In 2007, Bogomolov and Tschinkel [Reference Bogomolov, Tschinkel and Zannier3] used Raynaud’s theorem (the Manin–Mumford conjecture) to prove the following result.
Theorem 1.1 (Bogomolov–Tschinkel).
Let
![]() $E_1$
and
$E_1$
and
![]() $E_2$
be complex elliptic curves. For each
$E_2$
be complex elliptic curves. For each
![]() $i=1,2$
, let
$i=1,2$
, let
![]() $\pi _j\colon E_j\to {\mathbb {P}}^1$
be a degree-
$\pi _j\colon E_j\to {\mathbb {P}}^1$
be a degree-
![]() $2$
morphism that is even, and suppose that the branch loci of
$2$
morphism that is even, and suppose that the branch loci of
![]() $\pi _1$
and
$\pi _1$
and
![]() $\pi _2$
in
$\pi _2$
in
![]() ${\mathbb {P}}^1$
are different. Then
${\mathbb {P}}^1$
are different. Then
![]() $\pi _1(E_1[\infty ])\cap \pi _2(E_2[\infty ])$
is finite.
$\pi _1(E_1[\infty ])\cap \pi _2(E_2[\infty ])$
is finite.
We remark that if E is a complex elliptic curve and
![]() $\pi \colon E\to {\mathbb {P}}^1$
is an even degree-
$\pi \colon E\to {\mathbb {P}}^1$
is an even degree-
![]() $2$
map, then its branch locus is precisely
$2$
map, then its branch locus is precisely
![]() $\pi (E[2])\subseteq {\mathbb {P}}^1$
. The previous theorem motivated the following conjecture, which seems to have first appeared explicitly in joint works of Bogomolov, Fu and Tschinkel [Reference Bogomolov and Fu1–Reference Bogomolov, Tschinkel and Zannier3].
$\pi (E[2])\subseteq {\mathbb {P}}^1$
. The previous theorem motivated the following conjecture, which seems to have first appeared explicitly in joint works of Bogomolov, Fu and Tschinkel [Reference Bogomolov and Fu1–Reference Bogomolov, Tschinkel and Zannier3].
Conjecture 1.2 (Bogomolov–Fu–Tschinkel).
There is a constant c with the following property.
For any complex elliptic curves
![]() $E_1$
and
$E_1$
and
![]() $E_2$
, and for even degree-
$E_2$
, and for even degree-
![]() $2$
maps
$2$
maps
![]() $\pi _j\colon E_j\to {\mathbb {P}}^1$
whose branch loci in
$\pi _j\colon E_j\to {\mathbb {P}}^1$
whose branch loci in
![]() ${\mathbb {P}}^1$
are different,
${\mathbb {P}}^1$
are different,
![]() $\# (\pi _1(E_1[\infty ])\cap \pi _2(E_2[\infty ]))<c$
.
$\# (\pi _1(E_1[\infty ])\cap \pi _2(E_2[\infty ]))<c$
.
A first breakthrough was obtained in 2020 by DeMarco et al. [Reference DeMarco, Krieger and Ye4] when they proved the conjectured uniform bound in the case where
![]() $E_1$
and
$E_1$
and
![]() $E_2$
are given in Legendre form
$E_2$
are given in Legendre form
![]() $y^2=x(x-1)(x-\lambda )$
and
$y^2=x(x-1)(x-\lambda )$
and
![]() $\pi _j$
are the corresponding projections onto the x-coordinate. As noted in [Reference Fu and Stoll7], the Bogomolov–Fu–Tschinkel conjecture is now completely solved thanks to the recent proof of the uniform Manin–Mumford conjecture [Reference Dimitrov, Gao and Habegger6, Reference Gao, Ge and Kühne8, Reference Kühne10, Reference Kühne11, Reference Yuan14]. See also [Reference DeMarco and Mavraki5, Reference Poineau12] for alternative proofs of the Bogomolov–Fu–Tschinkel conjecture. In this work, we prove the following generalisation.
$\pi _j$
are the corresponding projections onto the x-coordinate. As noted in [Reference Fu and Stoll7], the Bogomolov–Fu–Tschinkel conjecture is now completely solved thanks to the recent proof of the uniform Manin–Mumford conjecture [Reference Dimitrov, Gao and Habegger6, Reference Gao, Ge and Kühne8, Reference Kühne10, Reference Kühne11, Reference Yuan14]. See also [Reference DeMarco and Mavraki5, Reference Poineau12] for alternative proofs of the Bogomolov–Fu–Tschinkel conjecture. In this work, we prove the following generalisation.
Theorem 1.3 (Main Theorem for torsion).
Let d be a positive integer. There is a constant
![]() $c_0(d)$
, depending only on d, which has the following property.
$c_0(d)$
, depending only on d, which has the following property.
For any complex elliptic curves
![]() $E_1$
and
$E_1$
and
![]() $E_2$
and nonconstant morphisms
$E_2$
and nonconstant morphisms
![]() $g_j\colon E_j\to {\mathbb {P}}^1$
of degree
$g_j\colon E_j\to {\mathbb {P}}^1$
of degree
![]() $\deg (g_j)\le d$
whose branch loci in
$\deg (g_j)\le d$
whose branch loci in
![]() ${\mathbb {P}}^1$
are different,
${\mathbb {P}}^1$
are different,
In a similar vein, if, instead of torsion points, we consider the Mordell–Weil group of elliptic curves over number fields, we obtain the following result.
Theorem 1.4 (Main Theorem for ranks).
Let d be a positive integer. There is a constant
![]() $\kappa (d)>0$
, depending only on d, with the following property.
$\kappa (d)>0$
, depending only on d, with the following property.
Let k be a number field and let
![]() $E_1$
and
$E_1$
and
![]() $E_2$
be elliptic curves over k. Let
$E_2$
be elliptic curves over k. Let
![]() $g_j\colon E_j\to {\mathbb {P}}^1$
be nonconstant morphisms defined over k of degree
$g_j\colon E_j\to {\mathbb {P}}^1$
be nonconstant morphisms defined over k of degree
![]() $\deg (g_j)\le d$
with different branch loci. Then
$\deg (g_j)\le d$
with different branch loci. Then
Thus, if two elliptic curves over a number field k have large intersection of the image of their k-rational points under rational maps to
![]() ${\mathbb {P}}^1$
of fixed degree and different branch loci, then at least one of the two elliptic curves has large rank over k. Thus, Theorem 1.4 is connected to the question of boundedness of ranks of elliptic curves over number fields.
${\mathbb {P}}^1$
of fixed degree and different branch loci, then at least one of the two elliptic curves has large rank over k. Thus, Theorem 1.4 is connected to the question of boundedness of ranks of elliptic curves over number fields.
To conclude this introduction, let us briefly describe our methods. The proof of the Bogomolov–Fu–Tschinkel conjecture applies the uniform Manin–Mumford conjecture to the curve
![]() $X\subseteq E_1\times E_2$
, which is defined by the equation
$X\subseteq E_1\times E_2$
, which is defined by the equation
![]() $\pi _1(P_1)=\pi _2(P_2)$
for
$\pi _1(P_1)=\pi _2(P_2)$
for
![]() $(P_1,P_2)\in E_1\times E_2$
. For this, one checks that X is an irreducible curve of geometric genus at least
$(P_1,P_2)\in E_1\times E_2$
. For this, one checks that X is an irreducible curve of geometric genus at least
![]() $2$
.
$2$
.
In the more general setting of Theorem 1.3, there is no reason for
![]() $g_1(P_1)=g_2(P_2)$
to define an irreducible curve in
$g_1(P_1)=g_2(P_2)$
to define an irreducible curve in
![]() $E_1\times E_2$
and one needs to ensure that all the irreducible components of the resulting algebraic set are curves of geometric genus at least
$E_1\times E_2$
and one needs to ensure that all the irreducible components of the resulting algebraic set are curves of geometric genus at least
![]() $2$
. This is achieved in an indirect way using Nevanlinna theory, for which we review the necessary background in Section 2. This approach originates in the authors’ proof of Bremner’s conjecture [Reference Garcia-Fritz and Pasten9]. In this way, we first obtain a purely geometric result in Section 3 (Theorem 3.3) from which Theorem 1.3 is deduced in Section 5 using the uniform Manin–Mumford conjecture (now a theorem). Finally, Theorem 1.4 is also proved in Section 5 by combining our geometric result with the uniform Mordell–Lang conjecture [Reference Dimitrov, Gao and Habegger6, Reference Gao, Ge and Kühne8, Reference Kühne10, Reference Yuan14] (see Section 4) instead of the uniform Manin–Mumford conjecture.
$2$
. This is achieved in an indirect way using Nevanlinna theory, for which we review the necessary background in Section 2. This approach originates in the authors’ proof of Bremner’s conjecture [Reference Garcia-Fritz and Pasten9]. In this way, we first obtain a purely geometric result in Section 3 (Theorem 3.3) from which Theorem 1.3 is deduced in Section 5 using the uniform Manin–Mumford conjecture (now a theorem). Finally, Theorem 1.4 is also proved in Section 5 by combining our geometric result with the uniform Mordell–Lang conjecture [Reference Dimitrov, Gao and Habegger6, Reference Gao, Ge and Kühne8, Reference Kühne10, Reference Yuan14] (see Section 4) instead of the uniform Manin–Mumford conjecture.
2 Nevanlinna theory
We use Landau’s notation o. Thus,
![]() $o(1)$
represents a function that tends to
$o(1)$
represents a function that tends to
![]() $0$
. In addition, the subscript ‘
$0$
. In addition, the subscript ‘
![]() $exc$
’ in inequalities and equalities between functions of a variable
$exc$
’ in inequalities and equalities between functions of a variable
![]() $r\in \mathbb {R}_{\ge 0}$
means that the claimed relationship holds for r outside a set of finite measure in
$r\in \mathbb {R}_{\ge 0}$
means that the claimed relationship holds for r outside a set of finite measure in
![]() $\mathbb {R}_{\ge 0}$
.
$\mathbb {R}_{\ge 0}$
.
In the first half of the 1920s, Nevanlinna developed a very successful theory to study value distribution of complex meromorphic functions. In this section, we recall some basic results of this theory; we refer the reader to [Reference Vojta, Colliot-Thélène, Swinnerton-Dyer and Vojta13] for a general reference.
Let
![]() $\mathscr {M}$
be the field of (possibly transcendental) complex meromorphic functions on
$\mathscr {M}$
be the field of (possibly transcendental) complex meromorphic functions on
![]() $\mathbb {C}$
. Given a nonconstant
$\mathbb {C}$
. Given a nonconstant
![]() $h\in \mathscr {M}$
, a point
$h\in \mathscr {M}$
, a point
![]() $\alpha \in {\mathbb {P}}^1(\mathbb {C})=\mathbb {C}\cup \{\infty \}$
and a real number
$\alpha \in {\mathbb {P}}^1(\mathbb {C})=\mathbb {C}\cup \{\infty \}$
and a real number
![]() $r\ge 0$
, we define
$r\ge 0$
, we define
where the case
![]() $h(z_0)=\infty $
is understood as the condition that h has a pole at
$h(z_0)=\infty $
is understood as the condition that h has a pole at
![]() $z_0$
. The truncated counting function
$z_0$
. The truncated counting function
![]() $N_h^{(1)}(\alpha ,r)$
is then defined as the logarithmic average
$N_h^{(1)}(\alpha ,r)$
is then defined as the logarithmic average
 $$ \begin{align*} N_h^{(1)}(\alpha,r) = \int_{0}^r(n_h^{(1)}(\alpha,t)-n_h^{(1)}(\alpha,0))\,\frac{dt}{t} + n_h^{(1)}(\alpha,0)\log r. \end{align*} $$
$$ \begin{align*} N_h^{(1)}(\alpha,r) = \int_{0}^r(n_h^{(1)}(\alpha,t)-n_h^{(1)}(\alpha,0))\,\frac{dt}{t} + n_h^{(1)}(\alpha,0)\log r. \end{align*} $$
Associated to every
![]() $h\in \mathscr {M}$
, there is the Nevanlinna height (or characteristic) function
$h\in \mathscr {M}$
, there is the Nevanlinna height (or characteristic) function
which has the basic property that it is bounded if h is constant; otherwise
![]() $T_f(r)$
grows to infinity as
$T_f(r)$
grows to infinity as
![]() $r\to \infty $
. We recall that the function
$r\to \infty $
. We recall that the function
![]() $T_h(r)$
is only defined up to adding a bounded function. Intuitively,
$T_h(r)$
is only defined up to adding a bounded function. Intuitively,
![]() $T_h(r)$
measures the complexity of h restricted to the disk
$T_h(r)$
measures the complexity of h restricted to the disk
![]() $\{z\in \mathbb {C}: \vert z\vert \le r\}$
as r grows. For our purposes, we do not need to recall the precise definition of
$\{z\in \mathbb {C}: \vert z\vert \le r\}$
as r grows. For our purposes, we do not need to recall the precise definition of
![]() $T_h(r)$
(which can be found, for example, in [Reference Vojta, Colliot-Thélène, Swinnerton-Dyer and Vojta13]), but instead we simply need its relationship to the truncated counting function, which is provided by the Second Main Theorem of Nevanlinna theory.
$T_h(r)$
(which can be found, for example, in [Reference Vojta, Colliot-Thélène, Swinnerton-Dyer and Vojta13]), but instead we simply need its relationship to the truncated counting function, which is provided by the Second Main Theorem of Nevanlinna theory.
Theorem 2.1 (Second Main Theorem).
Let
![]() $h\in \mathscr {M}$
be nonconstant and let
$h\in \mathscr {M}$
be nonconstant and let
![]() $\alpha _1,\ldots , \alpha _q$
be different points in
$\alpha _1,\ldots , \alpha _q$
be different points in
![]() ${\mathbb {P}}^1(\mathbb {C})$
. Then
${\mathbb {P}}^1(\mathbb {C})$
. Then
 $$ \begin{align*} \sum_{j=1}^q N^{(1)}_h(\alpha_j, r)\ge_{exc} (q-2+o(1))T_h(r). \end{align*} $$
$$ \begin{align*} \sum_{j=1}^q N^{(1)}_h(\alpha_j, r)\ge_{exc} (q-2+o(1))T_h(r). \end{align*} $$
In addition to the previous general result, we need another relationship between the Nevanlinna height and the truncated counting function in a special case.
Lemma 2.2 ([Reference Garcia-Fritz and Pasten9, Lemma 3.3]).
Let E be a complex elliptic curve and let
![]() $g\colon E\to {\mathbb {P}}^1$
be a nonconstant morphism of degree d. Let
$g\colon E\to {\mathbb {P}}^1$
be a nonconstant morphism of degree d. Let
![]() $\phi \colon \mathbb {C}\to E$
be a nonconstant holomorphic map and let
$\phi \colon \mathbb {C}\to E$
be a nonconstant holomorphic map and let
![]() $\alpha \in {\mathbb {P}}^1(\mathbb {C})$
. Consider the nonconstant meromorphic function
$\alpha \in {\mathbb {P}}^1(\mathbb {C})$
. Consider the nonconstant meromorphic function
![]() ${h=g\circ \phi \in \mathscr {M}}$
. Then
${h=g\circ \phi \in \mathscr {M}}$
. Then
We remark that our proof of the previous lemma in [Reference Garcia-Fritz and Pasten9] uses the Second Main Theorem for holomorphic maps to elliptic curves rather than the case of meromorphic functions cited above.
3 Geometric preliminaries
Let us fix some notation and assumptions for this section. Let
![]() $E_1$
and
$E_1$
and
![]() $E_2$
be complex elliptic curves. For
$E_2$
be complex elliptic curves. For
![]() $j=1,2$
, let
$j=1,2$
, let
![]() $g_j\colon E_j\to {\mathbb {P}}^1$
be a nonconstant morphism of degree
$g_j\colon E_j\to {\mathbb {P}}^1$
be a nonconstant morphism of degree
![]() $d_j$
. Suppose that
$d_j$
. Suppose that
![]() $g_1$
and
$g_1$
and
![]() $g_2$
have different branch loci in
$g_2$
have different branch loci in
![]() ${\mathbb {P}}^1$
. Let
${\mathbb {P}}^1$
. Let
![]() ${X\subseteq E_1\times E_2}$
be the one-dimensional algebraic set defined by the equation
${X\subseteq E_1\times E_2}$
be the one-dimensional algebraic set defined by the equation
![]() $g_1(P_1)=g_2(P_2)$
on
$g_1(P_1)=g_2(P_2)$
on
![]() ${(P_1,P_2)\in E_1\times E_2}$
: that is, X is the pre-image of the diagonal
${(P_1,P_2)\in E_1\times E_2}$
: that is, X is the pre-image of the diagonal
![]() $\Delta \subseteq {\mathbb {P}}^1\times {\mathbb {P}}^1$
via the map
$\Delta \subseteq {\mathbb {P}}^1\times {\mathbb {P}}^1$
via the map
![]() $G=(g_1,g_2)\colon E_1\times E_2\to {\mathbb {P}}^1\times {\mathbb {P}}^1$
.
$G=(g_1,g_2)\colon E_1\times E_2\to {\mathbb {P}}^1\times {\mathbb {P}}^1$
.
If
![]() $Z\subseteq E_1\times E_2$
is a one-dimensional algebraic set, we define its degree
$Z\subseteq E_1\times E_2$
is a one-dimensional algebraic set, we define its degree
![]() $\deg (Z)$
as the intersection number
$\deg (Z)$
as the intersection number
![]() $Z.(V_1+V_2)$
, where Z is seen as a reduced divisor, and we define
$Z.(V_1+V_2)$
, where Z is seen as a reduced divisor, and we define
![]() $V_1=\{0\}\times E_2$
and
$V_1=\{0\}\times E_2$
and
![]() $V_2=E_1\times \{0\}$
, where
$V_2=E_1\times \{0\}$
, where
![]() $0$
is the neutral point of the corresponding elliptic curve. Here, we remark that the divisor
$0$
is the neutral point of the corresponding elliptic curve. Here, we remark that the divisor
![]() $V_1+V_2$
on
$V_1+V_2$
on
![]() $E_1\times E_2$
is ample.
$E_1\times E_2$
is ample.
Lemma 3.1. We have
![]() $\deg (X)\le (d_1+d_2)d_1d_2$
.
$\deg (X)\le (d_1+d_2)d_1d_2$
.
Proof. Let
![]() $\Delta \subseteq {\mathbb {P}}^1\times {\mathbb {P}}^1$
be the diagonal and let
$\Delta \subseteq {\mathbb {P}}^1\times {\mathbb {P}}^1$
be the diagonal and let
![]() $L_1=\{p_1\}\times {\mathbb {P}}^1$
and
$L_1=\{p_1\}\times {\mathbb {P}}^1$
and
![]() $L_1={\mathbb {P}}^1\times \{p_2\}$
for a fixed choice of points
$L_1={\mathbb {P}}^1\times \{p_2\}$
for a fixed choice of points
![]() $p_1,p_2\in {\mathbb {P}}^1$
. Then
$p_1,p_2\in {\mathbb {P}}^1$
. Then
![]() $\Delta $
is linearly equivalent to
$\Delta $
is linearly equivalent to
![]() $L_1+L_2$
.
$L_1+L_2$
.
Note that
![]() $X=G^{-1}\Delta \le G^*\Delta $
as divisors, and by the projection formula,
$X=G^{-1}\Delta \le G^*\Delta $
as divisors, and by the projection formula,
 $$ \begin{align*} \begin{aligned} \deg(X)&\le \deg(G^*\Delta)\\ &=(G^*(L_1+L_2))\cdot (V_1+V_2)\\ &\leq G^*G_*(G^*(L_1+L_2)\cdot (V_1+V_2))\\ &=G^*((L_1+L_2)\cdot G_*(V_1+V_2))\\ &=d_1d_2(L_1+L_2)\cdot (d_2\cdot\{g_1(0)\}\times\mathbb{P}^1+d_1\cdot\mathbb{P}^1\times\{g_2(0)\})\\ &=d_1d_2(d_1+d_2).\\[-22pt] \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \deg(X)&\le \deg(G^*\Delta)\\ &=(G^*(L_1+L_2))\cdot (V_1+V_2)\\ &\leq G^*G_*(G^*(L_1+L_2)\cdot (V_1+V_2))\\ &=G^*((L_1+L_2)\cdot G_*(V_1+V_2))\\ &=d_1d_2(L_1+L_2)\cdot (d_2\cdot\{g_1(0)\}\times\mathbb{P}^1+d_1\cdot\mathbb{P}^1\times\{g_2(0)\})\\ &=d_1d_2(d_1+d_2).\\[-22pt] \end{aligned} \end{align*} $$
Before we give the main result of this section, we recall the Riemann–Hurwitz formula, which is useful in our argument.
Lemma 3.2 (Riemann–Hurwitz formula).
Let
![]() $Y_1$
and
$Y_1$
and
![]() $Y_2$
be smooth projective (complex) curves of genus
$Y_2$
be smooth projective (complex) curves of genus
![]() $\mathfrak {g}_1$
and
$\mathfrak {g}_1$
and
![]() $\mathfrak {g}_2$
, respectively, and let
$\mathfrak {g}_2$
, respectively, and let
![]() $g\colon Y_1\to Y_2$
be a nonconstant morphism of degree d. Let
$g\colon Y_1\to Y_2$
be a nonconstant morphism of degree d. Let
![]() $\alpha _1,\ldots , \alpha _m\in Y_2$
be all the branch values of g. Then
$\alpha _1,\ldots , \alpha _m\in Y_2$
be all the branch values of g. Then
 $$ \begin{align*} 2(\mathfrak{g}_1-1)=2d(\mathfrak{g}_2-1) + \sum_{j=1}^m (d-\#g^{-1}(\alpha_j)). \end{align*} $$
$$ \begin{align*} 2(\mathfrak{g}_1-1)=2d(\mathfrak{g}_2-1) + \sum_{j=1}^m (d-\#g^{-1}(\alpha_j)). \end{align*} $$
With this at hand, we can prove our geometric result.
Theorem 3.3. Every irreducible component of X is a curve of geometric genus at least
![]() $2$
.
$2$
.
Proof. Let
![]() $C\subseteq X$
be an irreducible component and, for the sake of contradiction, suppose that C has geometric genus
$C\subseteq X$
be an irreducible component and, for the sake of contradiction, suppose that C has geometric genus
![]() $0$
or
$0$
or
![]() $1$
. As
$1$
. As
![]() $C\subseteq E_1\times E_2$
, we see that, necessarily, C has geometric genus
$C\subseteq E_1\times E_2$
, we see that, necessarily, C has geometric genus
![]() $1$
, because the projection to at least one component
$1$
, because the projection to at least one component
![]() $E_i$
is nonconstant. Since elliptic curves can be uniformised by holomorphic functions from
$E_i$
is nonconstant. Since elliptic curves can be uniformised by holomorphic functions from
![]() $\mathbb {C}$
, we obtain a nonconstant holomorphic map
$\mathbb {C}$
, we obtain a nonconstant holomorphic map
![]() $\phi =(\phi _1,\phi _2)\colon \mathbb {C}\to C\subseteq E_1\times E_2$
, where at least one of
$\phi =(\phi _1,\phi _2)\colon \mathbb {C}\to C\subseteq E_1\times E_2$
, where at least one of
![]() $\phi _j\colon \mathbb {C}\to E_j$
is nonconstant. By the definition of X, we see that
$\phi _j\colon \mathbb {C}\to E_j$
is nonconstant. By the definition of X, we see that
![]() ${g_1\circ \phi _1=g_2\circ \phi _2}$
, and we conclude that both
${g_1\circ \phi _1=g_2\circ \phi _2}$
, and we conclude that both
![]() $\phi _j$
are nonconstant.
$\phi _j$
are nonconstant.
Let
![]() $h=g_1\circ \phi _1=g_2\circ \phi _2\in \mathscr {M}$
. Since
$h=g_1\circ \phi _1=g_2\circ \phi _2\in \mathscr {M}$
. Since
![]() $g_1$
and
$g_1$
and
![]() $g_2$
have different branch loci, we may assume, without loss of generality, that there is
$g_2$
have different branch loci, we may assume, without loss of generality, that there is
![]() $\beta \in {\mathbb {P}}^1$
that is a branch value of
$\beta \in {\mathbb {P}}^1$
that is a branch value of
![]() $g_2$
but not of
$g_2$
but not of
![]() $g_1$
. Let
$g_1$
. Let
![]() $\alpha _1,\ldots ,\alpha _m\in {\mathbb {P}}^1$
be the different branch values of
$\alpha _1,\ldots ,\alpha _m\in {\mathbb {P}}^1$
be the different branch values of
![]() $g_1$
.
$g_1$
.
By the Second Main Theorem 2.1 with
![]() $q=m+1$
,
$q=m+1$
,
 $$ \begin{align*} N^{(1)}_h(\beta,r)+\sum_{j=1}^m N^{(1)}_h(\alpha_j,r)\ge_{exc} (m-1+o(1))T_h(r). \end{align*} $$
$$ \begin{align*} N^{(1)}_h(\beta,r)+\sum_{j=1}^m N^{(1)}_h(\alpha_j,r)\ge_{exc} (m-1+o(1))T_h(r). \end{align*} $$
On the other hand, Lemma 2.2 gives
 $$ \begin{align*} N^{(1)}_h(\beta,r) =_{exc} \bigg(\frac{\# g_2^{-1}(\beta)}{d_2}+o(1)\bigg)T_h(r) \end{align*} $$
$$ \begin{align*} N^{(1)}_h(\beta,r) =_{exc} \bigg(\frac{\# g_2^{-1}(\beta)}{d_2}+o(1)\bigg)T_h(r) \end{align*} $$
and, for each
![]() $1\le j\le m$
, we similarly obtain
$1\le j\le m$
, we similarly obtain
 $$ \begin{align*} N^{(1)}_h(\alpha_j,r) =_{exc} \bigg(\frac{\# g_1^{-1}(\alpha_j)}{d_1}+o(1)\bigg)T_h(r). \end{align*} $$
$$ \begin{align*} N^{(1)}_h(\alpha_j,r) =_{exc} \bigg(\frac{\# g_1^{-1}(\alpha_j)}{d_1}+o(1)\bigg)T_h(r). \end{align*} $$
Putting all of this together, we find that
 $$ \begin{align*} \bigg(\frac{\# g_2^{-1}(\beta)}{d_2}+\sum_{j=1}^m\frac{\# g_1^{-1}(\alpha_j)}{d_1}+o(1)\bigg)T_h(r)\ge_{exc} (m-1+o(1))T_h(r). \end{align*} $$
$$ \begin{align*} \bigg(\frac{\# g_2^{-1}(\beta)}{d_2}+\sum_{j=1}^m\frac{\# g_1^{-1}(\alpha_j)}{d_1}+o(1)\bigg)T_h(r)\ge_{exc} (m-1+o(1))T_h(r). \end{align*} $$
Letting
![]() $r\to \infty $
, since h is nonconstant, we deduce that
$r\to \infty $
, since h is nonconstant, we deduce that
 $$ \begin{align*} m-1\le \frac{\# g_2^{-1}(\beta)}{d_2}+\sum_{j=1}^m\frac{\# g_1^{-1}(\alpha_j)}{d_1}. \end{align*} $$
$$ \begin{align*} m-1\le \frac{\# g_2^{-1}(\beta)}{d_2}+\sum_{j=1}^m\frac{\# g_1^{-1}(\alpha_j)}{d_1}. \end{align*} $$
Since
![]() $\beta $
is a branch value of
$\beta $
is a branch value of
![]() $g_2$
, we have
$g_2$
, we have
![]() $\# g_2^{-1}(\beta )<d_2$
, and hence
$\# g_2^{-1}(\beta )<d_2$
, and hence
 $$ \begin{align} m-1<1+\frac{1}{d_1}\sum_{j=1}^m \# g_1^{-1}(\alpha_j). \end{align} $$
$$ \begin{align} m-1<1+\frac{1}{d_1}\sum_{j=1}^m \# g_1^{-1}(\alpha_j). \end{align} $$
On the other hand, the Riemann–Hurwitz formula (in the form of Lemma 3.2) applied to
![]() $g_1\colon E_1\to {\mathbb {P}}^1$
gives
$g_1\colon E_1\to {\mathbb {P}}^1$
gives
 $$ \begin{align*} 0 = -2d_1 + \sum_{j=1}^m(d_1-\# g_1^{-1}(\alpha_j)) \end{align*} $$
$$ \begin{align*} 0 = -2d_1 + \sum_{j=1}^m(d_1-\# g_1^{-1}(\alpha_j)) \end{align*} $$
from which
 $$ \begin{align*} \frac{1}{d_1}\sum_{j=1}^m \# g_1^{-1}(\alpha_j)=m-2. \end{align*} $$
$$ \begin{align*} \frac{1}{d_1}\sum_{j=1}^m \# g_1^{-1}(\alpha_j)=m-2. \end{align*} $$
This contradicts the bound (3.1).
4 Uniform Mordell–Lang and Manin–Mumford
The rank of an abelian group
![]() $\Gamma $
, denoted by
$\Gamma $
, denoted by
![]() $\mathrm {rank}\, \Gamma $
, is defined as the dimension over
$\mathrm {rank}\, \Gamma $
, is defined as the dimension over
![]() $\mathbb {Q}$
of the vector space
$\mathbb {Q}$
of the vector space
![]() $\Gamma \otimes _{\mathbb {Z}} \mathbb {Q}$
.
$\Gamma \otimes _{\mathbb {Z}} \mathbb {Q}$
.
After the recent works [Reference Dimitrov, Gao and Habegger6, Reference Gao, Ge and Kühne8, Reference Kühne10, Reference Yuan14], the uniform Mordell–Lang conjecture is proved. Here, we recall the version obtained in [Reference Gao, Ge and Kühne8] in the case of (possibly singular) curves contained in abelian varieties.
Theorem 4.1 (Uniform Mordell–Lang for curves).
Let
![]() $n,D\ge 1$
be integers. There is a constant
$n,D\ge 1$
be integers. There is a constant
![]() $c(n,D)$
, depending only on n and D, with the following property.
$c(n,D)$
, depending only on n and D, with the following property.
Let A be an abelian variety over
![]() $\mathbb {C}$
of dimension n, let
$\mathbb {C}$
of dimension n, let
![]() $\mathscr {L}$
be an ample line sheaf on A and let
$\mathscr {L}$
be an ample line sheaf on A and let
![]() $X\subseteq A$
be a one-dimensional Zariski closed subset with
$X\subseteq A$
be a one-dimensional Zariski closed subset with
![]() $\deg _{\mathscr {L}}(X)\le D$
. Let
$\deg _{\mathscr {L}}(X)\le D$
. Let
![]() $\Gamma \le A(\mathbb {C})$
be a subgroup of finite rank and let
$\Gamma \le A(\mathbb {C})$
be a subgroup of finite rank and let
![]() $r=\mathrm {rank}\, \Gamma $
. If all irreducible components of X have geometric genus at least
$r=\mathrm {rank}\, \Gamma $
. If all irreducible components of X have geometric genus at least
![]() $2$
, then
$2$
, then
As usual,
![]() $\deg _{\mathscr {L}}(X)$
is defined as the intersection number of
$\deg _{\mathscr {L}}(X)$
is defined as the intersection number of
![]() $\mathscr {L}$
with X. Theorem 4.1 follows from Theorem 1.1 in [Reference Gao, Ge and Kühne8]; note that here we do not require that X is irreducible, but this case also follows from the same theorem because
$\mathscr {L}$
with X. Theorem 4.1 follows from Theorem 1.1 in [Reference Gao, Ge and Kühne8]; note that here we do not require that X is irreducible, but this case also follows from the same theorem because
![]() $\deg _{\mathscr {L}}(X)$
is additive on X and it is a strictly positive integer as
$\deg _{\mathscr {L}}(X)$
is additive on X and it is a strictly positive integer as
![]() $\mathscr {L}$
is ample.
$\mathscr {L}$
is ample.
In the special case where
![]() $\Gamma $
is the full torsion subgroup of A, one has
$\Gamma $
is the full torsion subgroup of A, one has
![]() $r=0$
and the previous result specialises to the uniform Manin–Mumford conjecture.
$r=0$
and the previous result specialises to the uniform Manin–Mumford conjecture.
Theorem 4.2 (Uniform Manin–Mumford for curves).
Let
![]() $n,D\ge 1$
be integers. There is a constant
$n,D\ge 1$
be integers. There is a constant
![]() $c(n,D)$
, depending only on n and D, with the following property.
$c(n,D)$
, depending only on n and D, with the following property.
Let A be an abelian variety over
![]() $\mathbb {C}$
of dimension n, let
$\mathbb {C}$
of dimension n, let
![]() $\mathscr {L}$
be an ample line sheaf on A and let
$\mathscr {L}$
be an ample line sheaf on A and let
![]() $X\subseteq A$
be a one-dimensional Zariski closed subset with
$X\subseteq A$
be a one-dimensional Zariski closed subset with
![]() $\deg _{\mathscr {L}}(X)\le D$
. Let
$\deg _{\mathscr {L}}(X)\le D$
. Let
![]() $A[\infty ]$
be the subgroup of all torsion points of
$A[\infty ]$
be the subgroup of all torsion points of
![]() $A(\mathbb {C})$
. If all irreducible components of X have geometric genus at least
$A(\mathbb {C})$
. If all irreducible components of X have geometric genus at least
![]() $2$
, then
$2$
, then
We point out that we use these results only when the abelian variety A is the product of two elliptic curves, so one may refer to [Reference Kühne11].
5 Torsion and ranks
In this section, we prove Theorems 1.3 and 1.4. For this, let us fix some common notation. Let k be
![]() $\mathbb {C}$
in the case of Theorem 1.3 or a number field in the case of Theorem 1.4. Let
$\mathbb {C}$
in the case of Theorem 1.3 or a number field in the case of Theorem 1.4. Let
![]() $E_1$
and
$E_1$
and
![]() $E_2$
be elliptic curves and let
$E_2$
be elliptic curves and let
![]() $g_j\colon E_j\to {\mathbb {P}}^1$
be morphisms of degrees
$g_j\colon E_j\to {\mathbb {P}}^1$
be morphisms of degrees
![]() $d_j\le d$
for
$d_j\le d$
for
![]() $j=1,2$
, all defined over k. We assume that the branch loci of
$j=1,2$
, all defined over k. We assume that the branch loci of
![]() $g_1$
and
$g_1$
and
![]() $g_2$
in
$g_2$
in
![]() ${\mathbb {P}}^1$
are different.
${\mathbb {P}}^1$
are different.
Let
![]() $G=(g_1,g_2)\colon E_1\times E_2\to {\mathbb {P}}^1\times {\mathbb {P}}^1$
, let
$G=(g_1,g_2)\colon E_1\times E_2\to {\mathbb {P}}^1\times {\mathbb {P}}^1$
, let
![]() $\Delta \subseteq {\mathbb {P}}^1\times {\mathbb {P}}^1$
be the diagonal and let
$\Delta \subseteq {\mathbb {P}}^1\times {\mathbb {P}}^1$
be the diagonal and let
![]() ${X=G^{-1}\Delta \subseteq E_1\times E_2}$
. We note that X is the locus of geometric points
${X=G^{-1}\Delta \subseteq E_1\times E_2}$
. We note that X is the locus of geometric points
![]() $(P_1,P_2)$
in
$(P_1,P_2)$
in
![]() $E_1\times E_2$
satisfying
$E_1\times E_2$
satisfying
![]() $g_1(P_1)=g_2(P_2)$
.
$g_1(P_1)=g_2(P_2)$
.
By Lemma 3.1,
![]() $\deg (X)\le d_1d_2(d_1+d_2)\le 2d^3$
, where
$\deg (X)\le d_1d_2(d_1+d_2)\le 2d^3$
, where
![]() $\deg (X)$
is the degree with respect to the ample divisor
$\deg (X)$
is the degree with respect to the ample divisor
![]() $V_1+V_2$
, as defined in Section 3. Furthermore, by Theorem 3.3, the (geometric) irreducible components of X have geometric genus at least
$V_1+V_2$
, as defined in Section 3. Furthermore, by Theorem 3.3, the (geometric) irreducible components of X have geometric genus at least
![]() $2$
.
$2$
.
Proof of Theorem 1.3.
Let
![]() $\Gamma =E_1[\infty ]\times E_2[\infty ]$
; this is the group of torsion points of the abelian surface
$\Gamma =E_1[\infty ]\times E_2[\infty ]$
; this is the group of torsion points of the abelian surface
![]() $E_1\times E_2$
. By Theorem 4.2,
$E_1\times E_2$
. By Theorem 4.2,
with
![]() $c(n,D)$
as in Theorem 4.2. We note that
$c(n,D)$
as in Theorem 4.2. We note that
and we obtain the result with
![]() $c_0(d)=c(2,2d^3)$
.
$c_0(d)=c(2,2d^3)$
.
Proof of Theorem 1.4.
The proof is very similar. Let
![]() $\Gamma =E_1(k)\times E_2(k)$
; by the Mordell–Weil theorem, this group is finitely generated and its rank is
$\Gamma =E_1(k)\times E_2(k)$
; by the Mordell–Weil theorem, this group is finitely generated and its rank is
![]() ${r=\mathrm {rank}\, E_1(k) + \mathrm {rank}\, E_2(k)}$
. By Theorem 4.1,
${r=\mathrm {rank}\, E_1(k) + \mathrm {rank}\, E_2(k)}$
. By Theorem 4.1,
with
![]() $c(n,D)$
as in Theorem 4.1. We note that
$c(n,D)$
as in Theorem 4.1. We note that
and we obtain the result with
![]() $\kappa (d)=1/\log c(2,2d^3)$
.
$\kappa (d)=1/\log c(2,2d^3)$
.
Acknowledgements
We thank Fabien Pazuki for pointing out some relevant references. We also thank the referee for useful and detailed comments.