Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-26T17:12:08.363Z Has data issue: false hasContentIssue false
  • English
  • Français

IMPROVED INEQUALITIES FOR THE NUMERICAL RADIUS: WHEN INVERSE COMMUTES WITH THE NORM

Part of: General theory of linear operators Normed linear spaces and Banach spaces; Banach lattices Basic linear algebra

Published online by Cambridge University Press:  02 February 2018

BRYAN E. CAIN Open the ORCID record for BRYAN E. CAIN [Opens in a new window]
BRYAN E. CAIN*
Affiliation:
OUCE, University of Oxford, Oxford, UK email [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

New inequalities relating the norm 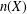$n(X)$ and the numerical radius 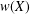$w(X)$ of invertible bounded linear Hilbert space operators were announced by Hosseini and Omidvar [‘Some inequalities for the numerical radius for Hilbert space operators’, Bull. Aust. Math. Soc.94 (2016), 489–496]. For example, they asserted that 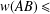$w(AB)\leq$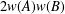$2w(A)w(B)$ for invertible bounded linear Hilbert space operators 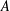$A$ and 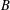$B$. We identify implicit hypotheses used in their discovery. The inequalities and their proofs can be made good by adding the extra hypotheses which take the form 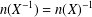$n(X^{-1})=n(X)^{-1}$. We give counterexamples in the absence of such additional hypotheses. Finally, we show that these hypotheses yield even stronger conclusions, for example, 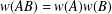$w(AB)=w(A)w(B)$.

Keywords

bounded linear operatorHilbert spacespectral radiusnumerical radiusnorm inequality

MSC classification

Primary: 47A62: Equations involving linear operators, with operator unknowns
Secondary: 15A60: Norms of matrices, numerical range, applications of functional analysis to matrix theory 46C15: Characterizations of Hilbert spaces 47A30: Norms (inequalities, more than one norm, etc.)
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 97 , Issue 2 , April 2018 , pp. 293 - 296
Copyright
© 2018 Australian Mathematical Publishing Association Inc. 

References

Berberian, S. K., ‘Approximate proper vectors’, Proc. Amer. Math. Soc. 13 (1962), 111–114.Google Scholar
Halmos, P. R., A Hilbert Space Problem Book (Van Nostrand, Princeton, NJ, 1967).Google Scholar
Hosseini, M. S. and Omidvar, M. E., ‘Some inequalities for the numerical radius for Hilbert space operators’, Bull. Aust. Math. Soc. 94 (2016), 489–496.Google Scholar
Li, C.-K., ‘Numerical radius’, in: Handbook of Linear Algebra, 2nd edn (ed. Hogben, L.) (Chapman and Hall, Boca Raton, FL, 2013), Section 25.4.Google Scholar