Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Gwóźdź-Łukawska, Gertruda
and
Jachymski, Jacek
2009.
IFS on a metric space with a graph structure and extensions of the Kelisky–Rivlin theorem.
Journal of Mathematical Analysis and Applications,
Vol. 356,
Issue. 2,
p.
453.
Mihail, Alexandru
and
Miculescu, Radu
2010.
Generalized IFSs on Noncompact Spaces.
Fixed Point Theory and Applications,
Vol. 2010,
Issue. 1,
Chiţescu, I.
Georgescu, H.
and
Miculescu, R.
2010.
Approximation of infinite dimensional fractals generated by integral equations.
Journal of Computational and Applied Mathematics,
Vol. 234,
Issue. 5,
p.
1417.
Dubbini, Nevio
Piccoli, Bendetto
and
Bicchi, Antonio
2010.
Left invertibility of discrete systems with finite inputs and quantised output.
International Journal of Control,
Vol. 83,
Issue. 4,
p.
798.
Dubbini, Nevio
Piccoli, Benedetto
and
Bicchi, Antonio
2011.
Left invertibility of discrete-time output-quantized systems: the linear case with finite inputs.
Mathematics of Control, Signals, and Systems,
Vol. 23,
Issue. 1-3,
p.
117.
Secelean, Nicolae Adrian
2012.
The Existence of the Attractor of Countable Iterated Function Systems.
Mediterranean Journal of Mathematics,
Vol. 9,
Issue. 1,
p.
61.
Miculescu, Radu
and
Ioana, Loredana
2012.
Some connections between the attractors of an IIFS S and the attractors of the sub-IFSs of S.
Fixed Point Theory and Applications,
Vol. 2012,
Issue. 1,
Jaroszewska, Joanna
2013.
A note on iterated function systems with discontinuous probabilities.
Chaos, Solitons & Fractals,
Vol. 49,
Issue. ,
p.
28.
Miculescu, Radu
and
Mihail, Alexandru
2013.
Alternative characterization of hyperbolic affine infinite iterated function systems.
Journal of Mathematical Analysis and Applications,
Vol. 407,
Issue. 1,
p.
56.
Secelean, Nicolae Adrian
2014.
Invariant Measure Associated with a Generalized Countable Iterated Function System.
Mediterranean Journal of Mathematics,
Vol. 11,
Issue. 2,
p.
361.
Miculescu, Radu
2014.
Generalized Iterated Function Systems with Place Dependent Probabilities.
Acta Applicandae Mathematicae,
Vol. 130,
Issue. 1,
p.
135.
Secelean, Nicolae-Adrian
2014.
Generalized iterated function systems on the spacel∞(X).
Journal of Mathematical Analysis and Applications,
Vol. 410,
Issue. 2,
p.
847.
Chiţescu, Ion
Ioana, Loredana
and
Miculescu, Radu
2014.
Type $${\mathcal{A}}$$ A Sets and the Attractors of Infinite Iterated Function Systems.
Results in Mathematics,
Vol. 66,
Issue. 3-4,
p.
511.
Dumitru, Dan
Ioana, Loredana
Sfetcu, Răzvan-Cornel
and
Strobin, Filip
2015.
Topological version of generalized (infinite) iterated function systems.
Chaos, Solitons & Fractals,
Vol. 71,
Issue. ,
p.
78.
Strobin, Filip
2015.
Attractors of generalized IFSs that are not attractors of IFSs.
Journal of Mathematical Analysis and Applications,
Vol. 422,
Issue. 1,
p.
99.
Balu, Rinju
Mathew, Sunil
and
Secelean, Nicolae Adrian
2017.
Separation properties of (n, m)-IFS attractors.
Communications in Nonlinear Science and Numerical Simulation,
Vol. 51,
Issue. ,
p.
160.
Arbieto, Alexander
Junqueira, André
and
Santiago, Bruno
2017.
On Weakly Hyperbolic Iterated Function Systems.
Bulletin of the Brazilian Mathematical Society, New Series,
Vol. 48,
Issue. 1,
p.
111.
Miculescu, Radu
and
Mihail, Alexandru
2018.
A Generalization for a Finite Family of Functions of the Converse of Browder’s Fixed Point Theorem.
Bulletin of the Brazilian Mathematical Society, New Series,
Vol. 49,
Issue. 4,
p.
673.
Chiţescu, Ion
Ioana, Loredana
Miculescu, Radu
and
Niţă, Lucian
2018.
Operators on Spaces of Functions and Measures. Vector Invariant (Fractal) Measures.
Results in Mathematics,
Vol. 73,
Issue. 4,
Fitzsimmons, Maxwell
and
Kunze, Herb
2018.
Recent Advances in Mathematical and Statistical Methods.
Vol. 259,
Issue. ,
p.
81.
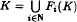 . Moreover, given σ ∈ ℕℕ and x ∈ X, the limit exists and does not depend on x. We also study separately the case in which (X, d) is Menger convex or compact. Finally, we answer a question posed by Máté concerning a finite iterated function system {F1,…, FN} with the property that each of Fi has a contractive fixed point.
. Moreover, given σ ∈ ℕℕ and x ∈ X, the limit exists and does not depend on x. We also study separately the case in which (X, d) is Menger convex or compact. Finally, we answer a question posed by Máté concerning a finite iterated function system {F1,…, FN} with the property that each of Fi has a contractive fixed point.

