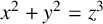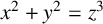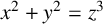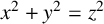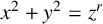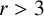1 Introduction
Diophantine equations are important in mathematics because of their historical significance, their central role in number theory and their applications in cryptography and other fields. Some Diophantine equations have no integral solution or only finitely many integral solutions, whereas some have infinitely many solutions, often characterised as parametrisations. One of the best known Diophantine equations is
![]() $x^2+y^2=z^2$
, whose positive integral solutions are known as Pythagorean triples. Some of its generalisations are
$x^2+y^2=z^2$
, whose positive integral solutions are known as Pythagorean triples. Some of its generalisations are
![]() $x^2+y^2=z^r$
and
$x^2+y^2=z^r$
and
![]() $x^2-y^2=z^r$
(
$x^2-y^2=z^r$
(
![]() $r\ge 2$
). In this paper, we consider the former one. Diophantine equations are used to characterise certain problems in Diophantine approximations. In [Reference Elsner, Komatsu, Shiokawa, Katsurada, Komatsu and Nakada4, Reference Elsner, Komatsu and Shiokawa5], we computed upper and lower bounds for the approximation of hyperbolic functions at points
$r\ge 2$
). In this paper, we consider the former one. Diophantine equations are used to characterise certain problems in Diophantine approximations. In [Reference Elsner, Komatsu, Shiokawa, Katsurada, Komatsu and Nakada4, Reference Elsner, Komatsu and Shiokawa5], we computed upper and lower bounds for the approximation of hyperbolic functions at points
![]() $1/s$
(
$1/s$
(
![]() $s=1,2,\ldots $
) by rationals
$s=1,2,\ldots $
) by rationals
![]() $x/y$
, such that x, y and z form Pythagorean triples. In [Reference Chaichana, Komatsu and Laohakosol2, Reference Elsner, Komatsu and Shiokawa6], we considered Diophantine approximations
$x/y$
, such that x, y and z form Pythagorean triples. In [Reference Chaichana, Komatsu and Laohakosol2, Reference Elsner, Komatsu and Shiokawa6], we considered Diophantine approximations
![]() $x/y$
to values of hyperbolic functions, where
$x/y$
to values of hyperbolic functions, where
![]() $(x,y,z)$
is the solution of certain Diophantine equations, including
$(x,y,z)$
is the solution of certain Diophantine equations, including
![]() $x^2+y^2=z^4$
.
$x^2+y^2=z^4$
.
For an integer
![]() $k\ge 2$
, consider a set of positive integers
$k\ge 2$
, consider a set of positive integers
![]() $A=\{a_1,\ldots ,a_k\}$
with
$A=\{a_1,\ldots ,a_k\}$
with
![]() $\gcd (A)=\gcd (a_1,\ldots ,a_k)=1$
. Finding the number
$\gcd (A)=\gcd (a_1,\ldots ,a_k)=1$
. Finding the number
![]() $d(n;A)=d(n;a_1,a_2,\ldots ,a_k)$
of nonnegative integral representations
$d(n;A)=d(n;a_1,a_2,\ldots ,a_k)$
of nonnegative integral representations
![]() $x_1,x_2,\ldots ,x_k$
to
$x_1,x_2,\ldots ,x_k$
to
![]() $a_1 x_1+a_2 x_2+\cdots +a_k x_k=n$
for a given positive integer n is an important and interesting problem. This number is often called the denumerant and is equal to the coefficient of
$a_1 x_1+a_2 x_2+\cdots +a_k x_k=n$
for a given positive integer n is an important and interesting problem. This number is often called the denumerant and is equal to the coefficient of
![]() $x^n$
in
$x^n$
in
![]() $1/(1-x^{a_1})(1-x^{a_2})\cdots (1-x^{a_k})$
(see [Reference Sylvester21]). For recent studies and references on the denumerant, see [Reference Komatsu10, Reference Liu and Xin17, Reference Liu, Xin and Zhang18].
$1/(1-x^{a_1})(1-x^{a_2})\cdots (1-x^{a_k})$
(see [Reference Sylvester21]). For recent studies and references on the denumerant, see [Reference Komatsu10, Reference Liu and Xin17, Reference Liu, Xin and Zhang18].
For a nonnegative integer p, define
![]() $S_p$
and
$S_p$
and
![]() $G_p$
by
$G_p$
by
so that
![]() $S_p\cup G_p=\mathbb N_0$
, which is the set of nonnegative integers. The set
$S_p\cup G_p=\mathbb N_0$
, which is the set of nonnegative integers. The set
![]() $S_p$
is called a p-numerical semigroup, because
$S_p$
is called a p-numerical semigroup, because
![]() $S(A)=S_0(A)$
is a numerical semigroup, and
$S(A)=S_0(A)$
is a numerical semigroup, and
![]() $G_p$
is the set of p-gaps. Define
$G_p$
is the set of p-gaps. Define
![]() $g_p(A)$
and
$g_p(A)$
and
![]() $n_p(A)$
by
$n_p(A)$
by
 $$ \begin{align*} g_p(A)=\max_{n\in G_p(A)}n,\quad n_p(A)=\sum_{n\in G_p(A)}1, \end{align*} $$
$$ \begin{align*} g_p(A)=\max_{n\in G_p(A)}n,\quad n_p(A)=\sum_{n\in G_p(A)}1, \end{align*} $$
respectively; these numbers are called the p-Frobenius number and the p-Sylvester number (or p-genus), respectively. When
![]() $p=0$
,
$p=0$
,
![]() $g(A)=g_0(A)$
and
$g(A)=g_0(A)$
and
![]() $n(A)=n_0(A)$
are the original Frobenius number and Sylvester number (or genus), respectively. More detailed descriptions of p-numerical semigroups and their symmetric properties can be found in [Reference Komatsu and Ying16].
$n(A)=n_0(A)$
are the original Frobenius number and Sylvester number (or genus), respectively. More detailed descriptions of p-numerical semigroups and their symmetric properties can be found in [Reference Komatsu and Ying16].
We are interested in explicit formulas for the Frobenius number and related values. For two variables,
![]() $A=\{a,b\}$
, it is known that
$A=\{a,b\}$
, it is known that
[Reference Sylvester21, Reference Sylvester22]. However, for three or more variables, the Frobenius number cannot be given by any set of closed formulas, which can be reduced to a finite set of polynomials [Reference Curtis3]. For three variables, various algorithms have been devised for finding the Frobenius number. Nevertheless, explicit closed formulas have been found only for some special cases (see [Reference Rosales, Branco and Torrão19] and references therein). Recently, the first author and his co-authors succeeded in giving the p-Frobenius number as a closed-form expression for the triangular number triplet [Reference Komatsu8], for repunits [Reference Komatsu9], Fibonacci triplets [Reference Komatsu and Ying14], Jacobsthal triplets [Reference Komatsu, Laishram and Punyani12, Reference Komatsu and Pita-Ruiz13] and arithmetic triplets [Reference Komatsu and Ying15].
In this paper, we study the numerical semigroup of the triples
![]() $(x,y,z)$
, satisfying the Diophantine equation
$(x,y,z)$
, satisfying the Diophantine equation
![]() $x^2+y^2=z^r$
(
$x^2+y^2=z^r$
(
![]() $r\ge 2$
). When
$r\ge 2$
). When
![]() $r=2$
, the Frobenius number of the Pythagorean triple is given in [Reference Gil, Han, Kim, Koo, Lee, Lee, Nam, Park and Park7]. Unlike the case of
$r=2$
, the Frobenius number of the Pythagorean triple is given in [Reference Gil, Han, Kim, Koo, Lee, Lee, Nam, Park and Park7]. Unlike the case of
![]() $x^2-y^2=z^r$
(
$x^2-y^2=z^r$
(
![]() $r\ge 2$
) in [Reference Yin and Komatsu23], it is more difficult to give a closed explicit formula for the Frobenius number of the triple from
$r\ge 2$
) in [Reference Yin and Komatsu23], it is more difficult to give a closed explicit formula for the Frobenius number of the triple from
![]() $x^2+y^2=z^r$
(
$x^2+y^2=z^r$
(
![]() $r\ge 2$
) for general r. So, in this paper, due to space limitations, we give the results for only
$r\ge 2$
) for general r. So, in this paper, due to space limitations, we give the results for only
![]() $r=3$
and
$r=3$
and
![]() $p=0$
. A detailed discussion, including the cases for
$p=0$
. A detailed discussion, including the cases for
![]() $r=4,5$
and for
$r=4,5$
and for
![]() $p>0$
, is given in [Reference Komatsu, Gupta and Upreti11].
$p>0$
, is given in [Reference Komatsu, Gupta and Upreti11].
2 Preliminaries
We introduce the p-Apéry set in order to obtain the formulas for
![]() $g_p(A)$
and
$g_p(A)$
and
![]() $n_p(A)$
. Without loss of generality, we assume that
$n_p(A)$
. Without loss of generality, we assume that
![]() $a_1=\min (A)$
.
$a_1=\min (A)$
.
Definition 2.1. Let p be a nonnegative integer. For a set of positive integers
![]() $A=\{a_1,a_2,\ldots ,a_\kappa \}$
with
$A=\{a_1,a_2,\ldots ,a_\kappa \}$
with
![]() $\gcd (A)=1$
and
$\gcd (A)=1$
and
![]() $a_1=\min (A)$
, we denote the p-Apéry set of A by
$a_1=\min (A)$
, we denote the p-Apéry set of A by
where each positive integer
![]() $m_i^{(p)}\ (0\le i\le a_1-1)$
satisfies the conditions
$m_i^{(p)}\ (0\le i\le a_1-1)$
satisfies the conditions
Note that
![]() $m_0^{(0)}$
is defined to be
$m_0^{(0)}$
is defined to be
![]() $0$
.
$0$
.
Lemma 2.2. Let k and p be integers with
![]() $k\ge 2$
and
$k\ge 2$
and
![]() $p\ge 0$
and assume that
$p\ge 0$
and assume that
![]() $\gcd (a_1,a_2,\ldots ,a_k)=1$
. Then
$\gcd (a_1,a_2,\ldots ,a_k)=1$
. Then
 $$ \begin{align} n_p(a_1,a_2,\ldots,a_k)&=\frac{1}{a_1}\sum_{j=0}^{a_1-1}m_j^{(p)}-\frac{a_1-1}{2}. \end{align} $$
$$ \begin{align} n_p(a_1,a_2,\ldots,a_k)&=\frac{1}{a_1}\sum_{j=0}^{a_1-1}m_j^{(p)}-\frac{a_1-1}{2}. \end{align} $$
Remark 2.3. When
![]() $p=0$
, the formulas (2.1) and (2.2) reduce to the formulas given by Brauer and Shockley [Reference Brauer and Shockley1] and Selmer [Reference Selmer20], respectively.
$p=0$
, the formulas (2.1) and (2.2) reduce to the formulas given by Brauer and Shockley [Reference Brauer and Shockley1] and Selmer [Reference Selmer20], respectively.
3
 $x^2+y^2=z^3$
$x^2+y^2=z^3$
For the solution of the Diophantine equation
![]() $x^2+y^2=z^r$
, we obtain the parametrisation
$x^2+y^2=z^r$
, we obtain the parametrisation
 $$ \begin{align*} x&=\sum_{k=0}^{\lfloor r/2\rfloor}(-1)^k\binom{r}{2 k}s^{r-2 k}t^{2 k},\\ y&=\sum_{k=0}^{\lfloor(r-1)/2\rfloor}(-1)^k\binom{r}{2 k+1}s^{r-2 k-1}t^{2 k+1},\\ z&=s^2+t^2, \end{align*} $$
$$ \begin{align*} x&=\sum_{k=0}^{\lfloor r/2\rfloor}(-1)^k\binom{r}{2 k}s^{r-2 k}t^{2 k},\\ y&=\sum_{k=0}^{\lfloor(r-1)/2\rfloor}(-1)^k\binom{r}{2 k+1}s^{r-2 k-1}t^{2 k+1},\\ z&=s^2+t^2, \end{align*} $$
where s and t are of opposite parity with
![]() $\gcd (s,t)=1$
.
$\gcd (s,t)=1$
.
The case
![]() $r=2$
has already been discussed in [Reference Gil, Han, Kim, Koo, Lee, Lee, Nam, Park and Park7], leading to
$r=2$
has already been discussed in [Reference Gil, Han, Kim, Koo, Lee, Lee, Nam, Park and Park7], leading to
Let
![]() $r=3$
. The triple of the Diophantine equation
$r=3$
. The triple of the Diophantine equation
![]() $x^2+y^2=z^3$
is parametrised by
$x^2+y^2=z^3$
is parametrised by
For convenience, we put
Since
![]() $\mathbf x,\mathbf y,\mathbf z>0$
and
$\mathbf x,\mathbf y,\mathbf z>0$
and
![]() $\gcd (\mathbf x,\mathbf y,\mathbf z)=1$
, we see that
$\gcd (\mathbf x,\mathbf y,\mathbf z)=1$
, we see that
![]() $s>\sqrt {3}t$
,
$s>\sqrt {3}t$
,
![]() $\gcd (s,t)=1$
and
$\gcd (s,t)=1$
and
![]() $s\not \equiv t\pmod {2}$
.
$s\not \equiv t\pmod {2}$
.
When
![]() $\mathbf x>\mathbf z$
, the Frobenius number of this triple is given in the following theorem.
$\mathbf x>\mathbf z$
, the Frobenius number of this triple is given in the following theorem.
Theorem 3.1. Suppose that
![]() $\mathbf x>\mathbf z$
. Then
$\mathbf x>\mathbf z$
. Then
 $$ \begin{align*} &g(s(s^2-3 t^2),t(3 s^2-t^2),s^2+t^2)\\&\quad=\begin{cases} &(s-1)s(s^2-3 t^2)+(s-1)t(3 s^2-t^2)-(s^2+t^2)\\ &\qquad\qquad\qquad\text{if } s>(1+\sqrt{2})t,\\ &(2 s+t-1)s(s^2-3 t^2)+(t-1)t(3 s^2-t^2)-(s^2+t^2)\\ &\qquad\qquad\qquad\text{if } 2 t<s<(1+\sqrt{2})t,\\ &(2 s+t-1)s(s^2-3 t^2)+(s-t-1)t(3 s^2-t^2)-(s^2+t^2)\\ &\qquad\qquad\qquad\text{if } (2+\sqrt{13})t/3<s<2 t,\\ &(5 s+3 t-1)s(s^2-3 t^2)+(2 t-s-1)t(3 s^2-t^2)-(s^2+t^2)\\ &\qquad\qquad\qquad\text{if } C_1 t<s<(2+\sqrt{13})t/3,\\ &(2 s+t-1)s(s^2-3 t^2)+(2 s-3 t-1)t(3 s^2-t^2)-(s^2+t^2)\\ &\qquad\qquad\qquad\text{if } (3+\sqrt{34})t/5<s<C_1 t,\\ &(7 s+4 t-1)s(s^2-3 t^2)+(2 t-s-1)t(3 s^2-t^2)-(s^2+t^2)\\ &\qquad\qquad\qquad\text{if } \sqrt{3}\,t<s<(3+\sqrt{34})t/5. \end{cases} \end{align*} $$
$$ \begin{align*} &g(s(s^2-3 t^2),t(3 s^2-t^2),s^2+t^2)\\&\quad=\begin{cases} &(s-1)s(s^2-3 t^2)+(s-1)t(3 s^2-t^2)-(s^2+t^2)\\ &\qquad\qquad\qquad\text{if } s>(1+\sqrt{2})t,\\ &(2 s+t-1)s(s^2-3 t^2)+(t-1)t(3 s^2-t^2)-(s^2+t^2)\\ &\qquad\qquad\qquad\text{if } 2 t<s<(1+\sqrt{2})t,\\ &(2 s+t-1)s(s^2-3 t^2)+(s-t-1)t(3 s^2-t^2)-(s^2+t^2)\\ &\qquad\qquad\qquad\text{if } (2+\sqrt{13})t/3<s<2 t,\\ &(5 s+3 t-1)s(s^2-3 t^2)+(2 t-s-1)t(3 s^2-t^2)-(s^2+t^2)\\ &\qquad\qquad\qquad\text{if } C_1 t<s<(2+\sqrt{13})t/3,\\ &(2 s+t-1)s(s^2-3 t^2)+(2 s-3 t-1)t(3 s^2-t^2)-(s^2+t^2)\\ &\qquad\qquad\qquad\text{if } (3+\sqrt{34})t/5<s<C_1 t,\\ &(7 s+4 t-1)s(s^2-3 t^2)+(2 t-s-1)t(3 s^2-t^2)-(s^2+t^2)\\ &\qquad\qquad\qquad\text{if } \sqrt{3}\,t<s<(3+\sqrt{34})t/5. \end{cases} \end{align*} $$
Here,
![]() $C_1=1.8139$
… is the positive real root of
$C_1=1.8139$
… is the positive real root of
![]() $3 x^4-7 x^3+6 x^2-3 x-5=0$
.
$3 x^4-7 x^3+6 x^2-3 x-5=0$
.
Remark 3.2. When
![]() $\mathbf x<\mathbf z$
, that is,
$\mathbf x<\mathbf z$
, that is,
![]() $s\sqrt {(s-1)/(3 s+1)}<t<s/\sqrt {3}$
, there is no uniform pattern for the Frobenius number. We need a separate discussion for each case. See [Reference Komatsu, Gupta and Upreti11] for details.
$s\sqrt {(s-1)/(3 s+1)}<t<s/\sqrt {3}$
, there is no uniform pattern for the Frobenius number. We need a separate discussion for each case. See [Reference Komatsu, Gupta and Upreti11] for details.
3.1 The case where
 $\sqrt {3}t<s<(2+\sqrt {3})t$
$\sqrt {3}t<s<(2+\sqrt {3})t$
We divide the discussion into five parts corresponding to the intervals in Figure 1.

Figure 1 The five intervals for
![]() $s/t$
considered in this section.
$s/t$
considered in this section.
If
![]() $\sqrt {3}t<s<(2+\sqrt {3})t$
, then
$\sqrt {3}t<s<(2+\sqrt {3})t$
, then
![]() $0<\mathbf x<\mathbf y$
. Hence,
$0<\mathbf x<\mathbf y$
. Hence,
![]() $\mathbf x<\mathbf z<\mathbf y$
or
$\mathbf x<\mathbf z<\mathbf y$
or
![]() $\mathbf z<\mathbf x<\mathbf y$
.
$\mathbf z<\mathbf x<\mathbf y$
.
First, consider
![]() $\mathbf z<\mathbf x<\mathbf y$
. Since
$\mathbf z<\mathbf x<\mathbf y$
. Since
![]() $(2 s+t)\mathbf x+(2 t-s)\mathbf y=2(s^2-s t-t^2)\mathbf z$
with
$(2 s+t)\mathbf x+(2 t-s)\mathbf y=2(s^2-s t-t^2)\mathbf z$
with
![]() $s^2-s t-t^2>(2-\sqrt {3})t^2$
,
$s^2-s t-t^2>(2-\sqrt {3})t^2$
,
Case 1:
![]() $(1+\sqrt {2})t<s<(2+\sqrt {3})t$
. The elements of the (
$(1+\sqrt {2})t<s<(2+\sqrt {3})t$
. The elements of the (
![]() $0$
-)Apéry set are shown in Figure 2, where each point
$0$
-)Apéry set are shown in Figure 2, where each point
![]() $(X,Y)$
corresponds to the expression
$(X,Y)$
corresponds to the expression
![]() $X\mathbf x+Y\mathbf y$
and the area of the (
$X\mathbf x+Y\mathbf y$
and the area of the (
![]() $0$
-)Apéry set is equal to
$0$
-)Apéry set is equal to
![]() $\mathbf z=s^2+t^2$
.
$\mathbf z=s^2+t^2$
.

Figure 2
![]() $\mathrm {Ap}_0(\mathbf x ,\mathbf y ,\mathbf z )$
when
$\mathrm {Ap}_0(\mathbf x ,\mathbf y ,\mathbf z )$
when
![]() $(1+\sqrt {2})t<s<(2+\sqrt {3})t$
.
$(1+\sqrt {2})t<s<(2+\sqrt {3})t$
.
Since
![]() $(1+\sqrt {2})t<s<(2+\sqrt {3})t$
, we see that
$(1+\sqrt {2})t<s<(2+\sqrt {3})t$
, we see that
![]() $(s+t)\mathbf x>(s-t)\mathbf y$
. Since
$(s+t)\mathbf x>(s-t)\mathbf y$
. Since
![]() $(s+t)\mathbf x\equiv (s-t)\mathbf y\pmod {\mathbf z }$
and
$(s+t)\mathbf x\equiv (s-t)\mathbf y\pmod {\mathbf z }$
and
![]() $s\mathbf x\equiv -t\mathbf y\pmod {\mathbf z}$
, the sequence
$s\mathbf x\equiv -t\mathbf y\pmod {\mathbf z}$
, the sequence
![]() $\{\ell \mathbf x\pmod {\mathbf z}\}_{\ell =0}^{\mathbf z-1}$
is given by
$\{\ell \mathbf x\pmod {\mathbf z}\}_{\ell =0}^{\mathbf z-1}$
is given by
 $$ \begin{align} &(0,0),(1,0),\ldots,(s+t-1,0),(0,s-t),(1,s-t),\ldots,(s-1,s-t),\notag\\ &(0,s-2 t),(1,s-2 t),\ldots,(s+t-1,s-2 t),\notag\\ &(0,2 s-3 t),(1,2 s-3 t),\ldots,(s-1,2 s-3 t),\notag\\ &(0,2 s-4 t),(1,2 s-4 t),\ldots,(s-1,2 s-4 t),\notag\\ &(0,2 s-5 t),(1,2 s-5 t),\ldots,(s+t-1,2 s-5 t)\notag\\ &(0,3 s-6 t),(1,3 s-6 t),\ldots,(s-1,3 s-6 t),\notag\\ &(0,3 s-7 t),(1,3 s-7 t),\ldots,(s-1,3 s-7 t)\notag\\ &\ldots,(s-1,s t-(s-1)t). \end{align} $$
$$ \begin{align} &(0,0),(1,0),\ldots,(s+t-1,0),(0,s-t),(1,s-t),\ldots,(s-1,s-t),\notag\\ &(0,s-2 t),(1,s-2 t),\ldots,(s+t-1,s-2 t),\notag\\ &(0,2 s-3 t),(1,2 s-3 t),\ldots,(s-1,2 s-3 t),\notag\\ &(0,2 s-4 t),(1,2 s-4 t),\ldots,(s-1,2 s-4 t),\notag\\ &(0,2 s-5 t),(1,2 s-5 t),\ldots,(s+t-1,2 s-5 t)\notag\\ &(0,3 s-6 t),(1,3 s-6 t),\ldots,(s-1,3 s-6 t),\notag\\ &(0,3 s-7 t),(1,3 s-7 t),\ldots,(s-1,3 s-7 t)\notag\\ &\ldots,(s-1,s t-(s-1)t). \end{align} $$
After
![]() $(s-1,s t-(s-1)t)$
, the next point adding
$(s-1,s t-(s-1)t)$
, the next point adding
![]() $\mathbf x \pmod {\mathbf z }$
is
$\mathbf x \pmod {\mathbf z }$
is
![]() $(0,0)$
. Note that the typical patterns in the sequence (3.2) are shown as follows: if
$(0,0)$
. Note that the typical patterns in the sequence (3.2) are shown as follows: if
![]() $k_1 s-k_2 t\le t-1$
, then the pattern is
$k_1 s-k_2 t\le t-1$
, then the pattern is
and if
![]() $k_1 s-k_2 t\ge t$
, then it is
$k_1 s-k_2 t\ge t$
, then it is
Since
![]() $\gcd (s,t)=1$
, all the points inside the area in Figure 2 appear in the sequence (3.2) just once. Since
$\gcd (s,t)=1$
, all the points inside the area in Figure 2 appear in the sequence (3.2) just once. Since
![]() $\gcd (\mathbf x ,\mathbf z )=1$
, the sequence
$\gcd (\mathbf x ,\mathbf z )=1$
, the sequence
![]() $\{\ell \mathbf x\pmod {\mathbf z }\}_{\ell =0}^{\mathbf z -1}$
is equivalent to the sequence
$\{\ell \mathbf x\pmod {\mathbf z }\}_{\ell =0}^{\mathbf z -1}$
is equivalent to the sequence
![]() $\{\ell \pmod {\mathbf z }\}_{\ell =0}^{\mathbf z -1}$
.
$\{\ell \pmod {\mathbf z }\}_{\ell =0}^{\mathbf z -1}$
.
Comparing the elements at
![]() $(s+t-1,t-1)$
and
$(s+t-1,t-1)$
and
![]() $(s-1,s-1)$
, taking possible maximal values, we find that the element at
$(s-1,s-1)$
, taking possible maximal values, we find that the element at
![]() $(s-1,s-1)$
is the largest in the Apéry set because
$(s-1,s-1)$
is the largest in the Apéry set because
 $$ \begin{align*} g(\mathbf x ,\mathbf y ,\mathbf z ) &=(s-1)\mathbf x +(s-1)\mathbf y -\mathbf z\\ &=(s-1)(s-t)(s^2+4 s t+t^2)-(s^2+t^2). \end{align*} $$
$$ \begin{align*} g(\mathbf x ,\mathbf y ,\mathbf z ) &=(s-1)\mathbf x +(s-1)\mathbf y -\mathbf z\\ &=(s-1)(s-t)(s^2+4 s t+t^2)-(s^2+t^2). \end{align*} $$
Case 2:
![]() $2 t<s<(\sqrt {2}+1)t$
. Now
$2 t<s<(\sqrt {2}+1)t$
. Now
![]() $(s+t)\mathbf x \equiv (s-t)\mathbf y \pmod {\mathbf z }$
but
$(s+t)\mathbf x \equiv (s-t)\mathbf y \pmod {\mathbf z }$
but
![]() $(s+t)\mathbf x <(s-t)\mathbf y $
. Nevertheless, by
$(s+t)\mathbf x <(s-t)\mathbf y $
. Nevertheless, by
![]() $(2 s+t)\mathbf x-(s-2 t)\mathbf y=2(s^2-s t-t^2)\mathbf z>0$
, we have
$(2 s+t)\mathbf x-(s-2 t)\mathbf y=2(s^2-s t-t^2)\mathbf z>0$
, we have
![]() $(2 s+t)\mathbf x \equiv (s-2 t)\mathbf y \pmod {\mathbf z }$
and
$(2 s+t)\mathbf x \equiv (s-2 t)\mathbf y \pmod {\mathbf z }$
and
![]() $(2 s+t)\mathbf x>(s-2 t)\mathbf y$
. For example,
$(2 s+t)\mathbf x>(s-2 t)\mathbf y$
. For example,
![]() $(s,t)=(9,4)$
satisfies this condition, so
$(s,t)=(9,4)$
satisfies this condition, so
![]() $(x,y,z)=(297,908,97)$
. Similarly, all the elements of the (
$(x,y,z)=(297,908,97)$
. Similarly, all the elements of the (
![]() $0$
-)Apéry set are given in Figure 3.
$0$
-)Apéry set are given in Figure 3.

Figure 3
![]() $\mathrm {Ap}_0(\mathbf x ,\mathbf y ,\mathbf z )$
when
$\mathrm {Ap}_0(\mathbf x ,\mathbf y ,\mathbf z )$
when
![]() $2 t<s<(\sqrt {2}+1)t$
.
$2 t<s<(\sqrt {2}+1)t$
.
Compare the elements at
![]() $(2 s+t-1,t-1)$
and
$(2 s+t-1,t-1)$
and
![]() $(s-1,s-t-1)$
, which take possible maximal values. Since the real roots of
$(s-1,s-t-1)$
, which take possible maximal values. Since the real roots of
![]() $-x^4+2 x^3-3 x^2+2 x+2=0$
are
$-x^4+2 x^3-3 x^2+2 x+2=0$
are
![]() $-0.4909$
and
$-0.4909$
and
![]() $1.4909$
, together with
$1.4909$
, together with
![]() $s>2 t$
, we see that
$s>2 t$
, we see that
and we find that the element at
![]() $(2 s+t-1,t-1)$
is the largest in the Apéry set. By (2.1) in Lemma 2.2,
$(2 s+t-1,t-1)$
is the largest in the Apéry set. By (2.1) in Lemma 2.2,
Case 3:
![]() $(2+\sqrt {13})t/3<s<2 t$
. For example,
$(2+\sqrt {13})t/3<s<2 t$
. For example,
![]() $(s,t)=(27,14)$
satisfies this condition, so
$(s,t)=(27,14)$
satisfies this condition, so
![]() $(x,y,z)=(3807,27874,925)$
.
$(x,y,z)=(3807,27874,925)$
.
By
![]() $(2+\sqrt {13})t/3<s$
, we have
$(2+\sqrt {13})t/3<s$
, we have
![]() $(3 s+2 t)\mathbf x-(2 s-3 t)\mathbf y=(3 s^2-4 s t-3 t^2)\mathbf z>0$
. So,
$(3 s+2 t)\mathbf x-(2 s-3 t)\mathbf y=(3 s^2-4 s t-3 t^2)\mathbf z>0$
. So,
![]() $(3 s+2 t)\mathbf x \equiv (2 s-3 t)\mathbf y \pmod {\mathbf z }$
and
$(3 s+2 t)\mathbf x \equiv (2 s-3 t)\mathbf y \pmod {\mathbf z }$
and
![]() $(3 s+2 t)\mathbf x>(2 s-3 t)\mathbf y$
. Together with (3.1), all the elements of the (
$(3 s+2 t)\mathbf x>(2 s-3 t)\mathbf y$
. Together with (3.1), all the elements of the (
![]() $0$
-)Apéry set are given in Figure 4.
$0$
-)Apéry set are given in Figure 4.

Figure 4
![]() $\mathrm {Ap}_0(\mathbf x ,\mathbf y ,\mathbf z )$
when
$\mathrm {Ap}_0(\mathbf x ,\mathbf y ,\mathbf z )$
when
![]() $(2+\sqrt {13})t/3<s<2 t$
.
$(2+\sqrt {13})t/3<s<2 t$
.
Compare the elements at
![]() $(3 s+2 t-1,2 t-s-1)$
and
$(3 s+2 t-1,2 t-s-1)$
and
![]() $(2 s+t-1,s-t-1)$
, which take the possible maximal values. We find that the element at
$(2 s+t-1,s-t-1)$
, which take the possible maximal values. We find that the element at
![]() $(s-1,s-1)$
is the largest in the Apéry set because
$(s-1,s-1)$
is the largest in the Apéry set because
![]() $(2+\sqrt {13})t/3<s<2 t$
and
$(2+\sqrt {13})t/3<s<2 t$
and
 $$ \begin{align*} &(2 s+t-1)\mathbf x+(s-t-1)\mathbf y -((3 s+2 t-1)\mathbf x+(2 t-s-1)\mathbf y)\\ &\quad=-(s^4- 5 s^3 t+6 s^2 t^2-s t^3-3 t^4)>0 \end{align*} $$
$$ \begin{align*} &(2 s+t-1)\mathbf x+(s-t-1)\mathbf y -((3 s+2 t-1)\mathbf x+(2 t-s-1)\mathbf y)\\ &\quad=-(s^4- 5 s^3 t+6 s^2 t^2-s t^3-3 t^4)>0 \end{align*} $$
for
![]() $C_2\, t<s<C_3\, t$
. Here,
$C_2\, t<s<C_3\, t$
. Here,
![]() $C_2\approx -0.5268$
and
$C_2\approx -0.5268$
and
![]() $C_3\approx 3.3968$
are the roots of
$C_3\approx 3.3968$
are the roots of
![]() $x^4- 5 x^3+6 x^2-x-3=0$
. By (2.1) in Lemma 2.2,
$x^4- 5 x^3+6 x^2-x-3=0$
. By (2.1) in Lemma 2.2,
Case 4:
![]() $(3+\sqrt {34})t/5<s<(2+\sqrt {13})t/3$
. For example,
$(3+\sqrt {34})t/5<s<(2+\sqrt {13})t/3$
. For example,
![]() $(s,t)=(24,13)$
satisfies this condition, so
$(s,t)=(24,13)$
satisfies this condition, so
![]() $(x,y,z)=(1656,20267,745)$
.
$(x,y,z)=(1656,20267,745)$
.
In this case,
![]() $(3 s+2 t)\mathbf x \equiv (2 s-3 t)\mathbf y \pmod {\mathbf z }$
but
$(3 s+2 t)\mathbf x \equiv (2 s-3 t)\mathbf y \pmod {\mathbf z }$
but
![]() $(3 s+2 t)\mathbf x <(2 s-3 t)\mathbf y $
. Nevertheless, since
$(3 s+2 t)\mathbf x <(2 s-3 t)\mathbf y $
. Nevertheless, since
![]() $(3+\sqrt {34})t/5<s$
, we have
$(3+\sqrt {34})t/5<s$
, we have
![]() $(5 s+3 t)\mathbf x-(3 s-5 t)\mathbf y=(5 s^2-6 s t-5 t^2)\mathbf z>0$
. So,
$(5 s+3 t)\mathbf x-(3 s-5 t)\mathbf y=(5 s^2-6 s t-5 t^2)\mathbf z>0$
. So,
![]() $(5 s+3 t)\mathbf x \equiv (3 s-5 t)\mathbf y \pmod {\mathbf z }$
and
$(5 s+3 t)\mathbf x \equiv (3 s-5 t)\mathbf y \pmod {\mathbf z }$
and
![]() $(5 s+3 t)\mathbf x>(3 s-5 t)\mathbf y$
. Together with (3.1), all the elements of the (
$(5 s+3 t)\mathbf x>(3 s-5 t)\mathbf y$
. Together with (3.1), all the elements of the (
![]() $0$
-)Apéry set are given in Figure 5.
$0$
-)Apéry set are given in Figure 5.

Figure 5
![]() $\mathrm {Ap}_0(\mathbf x ,\mathbf y ,\mathbf z )$
when
$\mathrm {Ap}_0(\mathbf x ,\mathbf y ,\mathbf z )$
when
![]() $(3+\sqrt {34})t/5<s<(2+\sqrt {13})t/3$
.
$(3+\sqrt {34})t/5<s<(2+\sqrt {13})t/3$
.
Comparing the elements at
![]() $(5 s+3 t-1,2 t-s-1)$
and
$(5 s+3 t-1,2 t-s-1)$
and
![]() $(2 s+t-1,2 s-3 t-1)$
, taking possible maximal values, we find that there are two possibilities. First, consider
$(2 s+t-1,2 s-3 t-1)$
, taking possible maximal values, we find that there are two possibilities. First, consider
 $$ \begin{align*} &(2 s+t-1)\mathbf x+(2 s-3 t-1)\mathbf y -((5 s+3 t-1)\mathbf x+(2 t-s-1)\mathbf y)\\ &\quad=-3 s^4+7 s^3 t-6 s^2 t^2+3 s t^3+5 t^4>0, \end{align*} $$
$$ \begin{align*} &(2 s+t-1)\mathbf x+(2 s-3 t-1)\mathbf y -((5 s+3 t-1)\mathbf x+(2 t-s-1)\mathbf y)\\ &\quad=-3 s^4+7 s^3 t-6 s^2 t^2+3 s t^3+5 t^4>0, \end{align*} $$
which is equivalent to
![]() $C_4\, t<s<C_1 t$
(where
$C_4\, t<s<C_1 t$
(where
![]() $C_4\approx -0.5553$
is also a root of
$C_4\approx -0.5553$
is also a root of
![]() $3 x^4-7 x^3+6 x^2-3 x-5=0$
). Restricting to the range in this case, if
$3 x^4-7 x^3+6 x^2-3 x-5=0$
). Restricting to the range in this case, if
![]() $1.7661\, t\approx (3+\sqrt {34})t/5<s<C_1 t$
, then, by (2.1) in Lemma 2.2,
$1.7661\, t\approx (3+\sqrt {34})t/5<s<C_1 t$
, then, by (2.1) in Lemma 2.2,
Otherwise, that is, if
![]() $C_1 t<s<(2+\sqrt {13})t/3\approx 1.8685\, t$
, then
$C_1 t<s<(2+\sqrt {13})t/3\approx 1.8685\, t$
, then
Case 5:
![]() $\sqrt {3}t<s<(3+\sqrt {34})t/5$
. For example,
$\sqrt {3}t<s<(3+\sqrt {34})t/5$
. For example,
![]() $(s,t)=(44,25)$
satisfies this condition, so
$(s,t)=(44,25)$
satisfies this condition, so
![]() $(x,y,z)=(2684,129575,2561)$
.
$(x,y,z)=(2684,129575,2561)$
.
In this case,
![]() $(5 s+3 t)\mathbf x \equiv (3 s-5 t)\mathbf y \pmod {\mathbf z }$
but
$(5 s+3 t)\mathbf x \equiv (3 s-5 t)\mathbf y \pmod {\mathbf z }$
but
![]() $(5 s+3 t)\mathbf x <(3 s-5 t)\mathbf y $
. Since
$(5 s+3 t)\mathbf x <(3 s-5 t)\mathbf y $
. Since
![]() $s>\sqrt {3}t\ (\approx 1.732\,t)>(4+\sqrt {65})t/7\ (\approx 1.723\,t)$
, we have
$s>\sqrt {3}t\ (\approx 1.732\,t)>(4+\sqrt {65})t/7\ (\approx 1.723\,t)$
, we have
![]() $(7 s+4 t)\mathbf x-(4 s-7 t)\mathbf y=(7 s^2 - 8 s t - 7 t^2)\mathbf z>0$
. So,
$(7 s+4 t)\mathbf x-(4 s-7 t)\mathbf y=(7 s^2 - 8 s t - 7 t^2)\mathbf z>0$
. So,
![]() $(7 s+4 t)\mathbf x \equiv (4 s-7 t)\mathbf y \pmod {\mathbf z }$
and
$(7 s+4 t)\mathbf x \equiv (4 s-7 t)\mathbf y \pmod {\mathbf z }$
and
![]() $(7 s+4 t)\mathbf x>(4 s-7 t)\mathbf y$
. Together with (3.1), all the elements of the (
$(7 s+4 t)\mathbf x>(4 s-7 t)\mathbf y$
. Together with (3.1), all the elements of the (
![]() $0$
-)Apéry set are given as Figure 6.
$0$
-)Apéry set are given as Figure 6.

Figure 6
![]() $\mathrm {Ap}_0(\mathbf x ,\mathbf y ,\mathbf z )$
when
$\mathrm {Ap}_0(\mathbf x ,\mathbf y ,\mathbf z )$
when
![]() $\sqrt {3}t<s<(3+\sqrt {34})t/5$
.
$\sqrt {3}t<s<(3+\sqrt {34})t/5$
.
Comparing the elements at
![]() $(7 s+4 t-1,2 t-s-1)$
and
$(7 s+4 t-1,2 t-s-1)$
and
![]() $(2 s+t-1,3 s-5 t-1)$
, taking possible maximal values, we find that the element at
$(2 s+t-1,3 s-5 t-1)$
, taking possible maximal values, we find that the element at
![]() $(7 s+4 t-1,2 t-s-1)$
is the largest in the Apéry set because, from
$(7 s+4 t-1,2 t-s-1)$
is the largest in the Apéry set because, from
![]() $\sqrt {3}t<s<(3+\sqrt {34})t/5$
,
$\sqrt {3}t<s<(3+\sqrt {34})t/5$
,
 $$ \begin{align*} &(2 s+t-1)\mathbf x+(3 s-5 t-1)\mathbf y -((7 s+4 t-1)\mathbf x+(2 t-s-1)\mathbf y)\\ &\quad=-5 s^4+9 s^3 t-6 s^2 t^2+5 s t^3+7 t^4<0. \end{align*} $$
$$ \begin{align*} &(2 s+t-1)\mathbf x+(3 s-5 t-1)\mathbf y -((7 s+4 t-1)\mathbf x+(2 t-s-1)\mathbf y)\\ &\quad=-5 s^4+9 s^3 t-6 s^2 t^2+5 s t^3+7 t^4<0. \end{align*} $$
Note that
![]() $-5 x^4+9 x^3-6 x^2+5 x+7=0$
has real roots at
$-5 x^4+9 x^3-6 x^2+5 x+7=0$
has real roots at
![]() $0.5702$
and
$0.5702$
and
![]() $1.71692$
and
$1.71692$
and
![]() $s>\sqrt {3}t=1.732 t$
. By (2.1) in Lemma 2.2,
$s>\sqrt {3}t=1.732 t$
. By (2.1) in Lemma 2.2,
3.2 The case
 $s>(2+\sqrt {3})t$
$s>(2+\sqrt {3})t$
If
![]() $s>(2+\sqrt {3})t$
, then
$s>(2+\sqrt {3})t$
, then
![]() $\mathbf z<\mathbf y<\mathbf x$
. The elements of the (
$\mathbf z<\mathbf y<\mathbf x$
. The elements of the (
![]() $0$
-)Apéry set are given in Figure 7, where each point
$0$
-)Apéry set are given in Figure 7, where each point
![]() $(Y,X)$
corresponds to the expression
$(Y,X)$
corresponds to the expression
![]() $Y \mathbf y +X \mathbf x $
and the area of the (
$Y \mathbf y +X \mathbf x $
and the area of the (
![]() $0$
-)Apéry set is equal to
$0$
-)Apéry set is equal to
![]() $\mathbf z=s^2+t^2$
.
$\mathbf z=s^2+t^2$
.

Figure 7
![]() $\mathrm {Ap}_0(\mathbf x ,\mathbf y ,\mathbf z )$
when
$\mathrm {Ap}_0(\mathbf x ,\mathbf y ,\mathbf z )$
when
![]() $s>(2+\sqrt {3})t$
.
$s>(2+\sqrt {3})t$
.
Since
![]() $s\mathbf y-t\mathbf x=s t\mathbf z$
, we have
$s\mathbf y-t\mathbf x=s t\mathbf z$
, we have
![]() $s\mathbf y \equiv t\mathbf x \pmod {\mathbf z }$
and
$s\mathbf y \equiv t\mathbf x \pmod {\mathbf z }$
and
![]() $s\mathbf y>t\mathbf x $
. By using an additional relationship
$s\mathbf y>t\mathbf x $
. By using an additional relationship
![]() $t\mathbf y+s\mathbf x=(s-t)(s+t)\mathbf z$
, it can be shown that the sequence
$t\mathbf y+s\mathbf x=(s-t)(s+t)\mathbf z$
, it can be shown that the sequence
![]() $\{\ell \mathbf y\pmod {\mathbf z }\}_{\ell =0}^{\mathbf z -1}$
matches the sequence
$\{\ell \mathbf y\pmod {\mathbf z }\}_{\ell =0}^{\mathbf z -1}$
matches the sequence
![]() $\{\ell \pmod {\mathbf z }\}_{\ell =0}^{\mathbf z -1}$
(see [Reference Komatsu, Gupta and Upreti11]).
$\{\ell \pmod {\mathbf z }\}_{\ell =0}^{\mathbf z -1}$
(see [Reference Komatsu, Gupta and Upreti11]).
Since
![]() $s>(2+\sqrt {3})t$
, we have
$s>(2+\sqrt {3})t$
, we have
![]() $(s-1)\mathbf y+(s-1)\mathbf x>(t-1)\mathbf y+(s+t-1)\mathbf x$
. Hence, by (2.1) in Lemma 2.2,
$(s-1)\mathbf y+(s-1)\mathbf x>(t-1)\mathbf y+(s+t-1)\mathbf x$
. Hence, by (2.1) in Lemma 2.2,
4 Final comments
When
![]() $\mathbf x<\mathbf z<\mathbf y$
, or
$\mathbf x<\mathbf z<\mathbf y$
, or
![]() $s(s^2-3 t^2)<\mathbf z $
and
$s(s^2-3 t^2)<\mathbf z $
and
![]() $s>\sqrt {3}t$
, we need a more precise discussion in each special case (see [Reference Komatsu, Gupta and Upreti11]).
$s>\sqrt {3}t$
, we need a more precise discussion in each special case (see [Reference Komatsu, Gupta and Upreti11]).
The detail, the proof and the results including the cases
![]() $r=4,5$
are recorded in [Reference Komatsu, Gupta and Upreti11], although the structures for
$r=4,5$
are recorded in [Reference Komatsu, Gupta and Upreti11], although the structures for
![]() $r=4,5$
are not similar to that for
$r=4,5$
are not similar to that for
![]() $r=3$
. When
$r=3$
. When
![]() $p>0$
, the formulas for p-Frobenius numbers and p-Sylvester numbers are obtained, although there are many different situations. See [Reference Komatsu, Gupta and Upreti11] for the details.
$p>0$
, the formulas for p-Frobenius numbers and p-Sylvester numbers are obtained, although there are many different situations. See [Reference Komatsu, Gupta and Upreti11] for the details.
When
![]() $r\ge 6$
, we can also obtain the Frobenius numbers of the triple for
$r\ge 6$
, we can also obtain the Frobenius numbers of the triple for
![]() $x^2+y^2=z^r$
. However, we need to discuss the cases for each specific value of r.
$x^2+y^2=z^r$
. However, we need to discuss the cases for each specific value of r.
Acknowledgment
The authors thank the referee for carefully reading the manuscript and for giving constructive comments.