Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-18T17:44:40.859Z Has data issue: false hasContentIssue false
  • English
  • Français

FINITE GROUPS WHOSE NONCENTRAL COMMUTING ELEMENTS HAVE CENTRALIZERS OF EQUAL SIZE

Part of: Representation theory of groups Structure and classification of infinite or finite groups

Published online by Cambridge University Press:  07 July 2010

SILVIO DOLFI ,
MARCEL HERZOG  and
ENRICO JABARA
SILVIO DOLFI
Affiliation:
Dipartimento di Matematica U. Dini, Università degli Studi di Firenze, viale Morgagni 67/a, 50134 Firenze, Italy (email: [email protected])
MARCEL HERZOG*
Affiliation:
Department of Mathematics, Raymond and Beverly Sackler Faculty of Exact Sciences, Tel Aviv University, Tel Aviv, Israel (email: [email protected])
ENRICO JABARA
Affiliation:
Dipartimento di Matematica Applicata, Università di Ca’Foscari, 30123 Venezia, Italy (email: [email protected])
*
✉For correspondence; e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

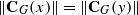A finite group is called a CH-group if for every x,y∈G∖Z(G), xy=yx implies that . Applying results of Schmidt [‘Zentralisatorverbände endlicher Gruppen’, Rend. Sem. Mat. Univ. Padova44 (1970), 97–131] and Rebmann [‘F-Gruppen’, Arch. Math. 22 (1971), 225–230] concerning CA-groups and F-groups, the structure of CH-groups is determined, up to that of CH-groups of prime-power order. Upper bounds are found for the derived length of nilpotent and solvable CH-groups.

Keywords

centralizersorder of centralizersF-groupsCA-groups

MSC classification

Secondary: 20E34: General structure theorems 20D60: Arithmetic and combinatorial problems 20D15: Nilpotent groups, $p$-groups
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 82 , Issue 2 , October 2010 , pp. 293 - 304
Copyright
Copyright © Australian Mathematical Publishing Association Inc. 2010

Footnotes

The first and the third authors were partially supported by the MIUR project ‘Teoria dei gruppi e applicazioni’.

References

[1] GAP– Groups, Algorithms and Programming, Version 4.4.12 (2008), http://www.gap-system.org.Google Scholar
[2]Isaacs, I. M., ‘Subgroups generated by small classes in finite groups’, Proc. Amer. Math. Soc. 136 (2008), 2299–2301.CrossRefGoogle Scholar
[3]Ishikawa, K., ‘On finite p-groups which have only two conjugacy lengths’, Israel J. Math. 129 (2002), 119–123.CrossRefGoogle Scholar
[4]Ito, N., ‘On finite groups with given conjugate type, I’, Nagoya J. Math. 6 (1953), 17–28.Google Scholar
[5]Mann, A., ‘Conjugacy classes in finite groups’, Israel J. Math. 31 (1978), 78–84.Google Scholar
[6]Mann, A., ‘Elements of minimal breadth in finite p-groups and Lie algebras’, J. Aust. Math. Soc. 81 (2006), 209–214.Google Scholar
[7]Rebmann, J., ‘F-Gruppen’, Arch. Math. 22 (1971), 225–230.CrossRefGoogle Scholar
[8]Robinson, D. J. S., Finiteness Conditions and General Soluble Groups, Part 2 (Springer, Berlin, 1972).Google Scholar
[9]Robinson, D. J. S., A Course in the Theory of Groups (Springer, Berlin, 1982).CrossRefGoogle Scholar
[10]Schmidt, R., ‘Zentralisatorverbände endlicher Gruppen’, Rend. Sem. Mat. Univ. Padova 44 (1970), 97–131.Google Scholar
[11]Schmidt, R., Subgroup Lattices of Groups (De Gruyter, Berlin, 1994).CrossRefGoogle Scholar