Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-28T20:09:44.507Z Has data issue: false hasContentIssue false
  • English
  • Français

THE FACTORIAL CONJECTURE AND IMAGES OF LOCALLY NILPOTENT DERIVATIONS

Part of: Affine geometry Differential algebra

Published online by Cambridge University Press:  20 May 2019

DAYAN LIU  and
XIAOSONG SUN Open the ORCID record for XIAOSONG SUN [Opens in a new window]
DAYAN LIU
Affiliation:
School of Mathematics, Jilin University, Changchun, 130012, China email [email protected]
XIAOSONG SUN*
Affiliation:
School of Mathematics, Jilin University, Changchun, 130012, China email [email protected]
*
✉[email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The factorial conjecture was proposed by van den Essen et al. [‘On the image conjecture’, J. Algebra 340(1) (2011), 211–224] to study the image conjecture, which arose from the Jacobian conjecture. We show that the factorial conjecture holds for all homogeneous polynomials in two variables. We also give a variation of the result and use it to show that the image of any linear locally nilpotent derivation of 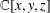$\mathbb{C}[x,y,z]$ is a Mathieu–Zhao subspace.

Keywords

factorial conjectureJacobian conjecturelocally nilpotent derivationsMathieu–Zhao subspaces

MSC classification

Primary: 14R15: Jacobian problem
Secondary: 13N15: Derivations 14R10: Affine spaces (automorphisms, embeddings, exotic structures, cancellation problem)
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 101 , Issue 1 , February 2020 , pp. 71 - 79
Copyright
© 2019 Australian Mathematical Publishing Association Inc. 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

This work was supported by the NSF of China (grants 11871241 and 11771176), the EDJP of China (JJKH20190185KJ) and the China Scholarship Council.

References

Bass, H., Connel, E. and Wright, D., ‘The Jacobian conjecture: reduction of degree and formal expansion of the inverse’, Bull. Amer. Math. Soc. 7 (1982), 287–330.10.1090/S0273-0979-1982-15032-7Google Scholar
Edo, E. and van den Essen, A., ‘The strong factorial conjecture’, J. Algebra 397 (2014), 443–456.10.1016/j.jalgebra.2013.09.011Google Scholar
van den Essen, A., Polynomial Automorphisms and the Jacobian Conjecture, Progress in Mathematics, 190 (Birkhäuser, Basel–Boston–Berlin, 2000).10.1007/978-3-0348-8440-2Google Scholar
van den Essen, A. and Sun, X., ‘Monomial preserving derivations and Mathieu–Zhao subspaces’, J. Pure Appl. Algebra 222 (2018), 3219–3223.Google Scholar
van den Essen, A., Wright, D. and Zhao, W., ‘Images of locally finite derivations of polynomial algebras in two variables’, J. Pure Appl. Algebra 215(9) (2011), 2130–2134.10.1016/j.jpaa.2010.12.002Google Scholar
van den Essen, A., Wright, D. and Zhao, W., ‘On the image conjecture’, J. Algebra 340(1) (2011), 211–224.Google Scholar
van den Essen, A. and Zhao, W., ‘Mathieu subspaces of univariate polynomial algebra’, J. Pure Appl. Algebra 217(9) (2013), 1316–1324.10.1016/j.jpaa.2012.10.006Google Scholar
Françoise, J. P., Pakovich, F., Yomdin, Y. and Zhao, W., ‘Moment vanishing problem and positivity: some examples’, Bull. Sci. Math. 135 (2011), 10–32.Google Scholar
Liu, D. and Sun, X., ‘Images of higher-order differential operators of polynomial algebras’, Bull. Aust. Math. Soc. 96(2) (2017), 205–211.10.1017/S0004972717000454Google Scholar
Sun, X., ‘Images of derivations of polynomial algebras with divergence zero’, J. Algebra 492 (2017), 414–418.10.1016/j.jalgebra.2017.09.020Google Scholar
Zhao, W., ‘Images of commuting differential operators of order one with constant leading coefficients’, J. Algebra 324(2) (2010), 231–247.Google Scholar
Zhao, W., ‘Generalizations of the image conjecture and the Mathieu conjecture’, J. Pure Appl. Algebra 214(7) (2010), 1200–1216.10.1016/j.jpaa.2009.10.007Google Scholar
Zhao, W., ‘Mathieu subspaces of associative algebras’, J. Algebra 350(1) (2012), 245–272.10.1016/j.jalgebra.2011.09.036Google Scholar
Zhao, W., ‘Some open problems on locally finite or locally nilpotent derivations and 𝜀-derivations’, Contemp. Math. 20(4) (2019), Article ID 1750056.Google Scholar